Василий Налимов - Разбрасываю мысли

Еще раньше, в начале нашего века Д’Арси Томпсону [Thompson D’A. W., 1942] удалось показать, что формообразование может быть интерпретировано как изменение метрики того пространства, в котором задан несколько схематизированный двухмерный образ того или иного животного. На рис. 4 показано, как различные формы панциря краба могут быть получены из одного – исходного, заданного в равномерной прямоугольной сетке, путем ее сжатия или растягивания, с обращением к косоугольным или криволинейным координатам. На рис. 5 путем аналогичных геометрических преобразований получены различные формы рыб. В работе [Barger, 1974] мы обнаружили еще одно изображение похожей пространственной трансформации двухмерного образа животного (рис. 6). В центре рисунка в линейных координатах изображена свинья, в других координатных осях она превращается в бизона, бабуина и еще в каких-то других, не опознаваемых, т. е. эволюционно не реализовавшихся, но потенциально возможных животных [89]. Этот рисунок, демонстрировавшийся на одной из конференций по физике элементарных частиц и высоких энергий, показывает искусство игры размерностями координатных осей, задающими метрику пространства. Прослеживая путь, идущий от Д’Арси Томпсона, мы должны упомянуть книгу [Bookstein, 1978] [90](она содержит библиографию в 212 наименований), статью [Todd et al., 1980] и, наконец, книгу нашего биогеометра С.В. Петухова [1981], в которой основное внимание уделяется конформным (круговым) симметриям и числам Фибоначчи в биологических телах и, в частности, в кинематической схеме тела человека и животных. Фундаментальное значение приобретает представление о неевклидовом базисе законов морфогенеза. Особенно удачным в книге С.В. Пе-тухова оказался поиск проективных симметрий в расположении пяти оконечных точек человеческого тела. Выяснилось (рис. 7), что в онтогенетической трансформации геометрии тела сохраняется та самая пентасимметрия, которая имеет место в пятилепестковых цветках растений, в телах морских звезд и пр. [91]Из рисунка следует, что приведенная там пентасимметрическая трансформация может быть интерпретирована и как трансформация [92], обусловленная изменением метрики того пространства, в котором задана форма.

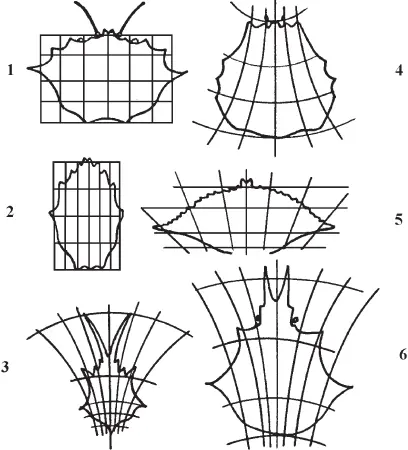
Рис. 4. Панцири различных крабов: 1 – Geryon; 2 – Corystes; 3 – Scyramathia; 4 – Paralomis; 5 – Lupa; 6 – Chorinus [Thompson D’A. W., 1942].

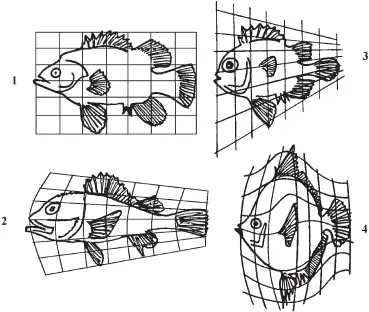
Рис. 5. Формы рыб: 1 – Polyprion; 2 – Pseudopricanthus; 3 – Scorpena; 4 – Antigonia capros [Thompson D’A. W., 1942].

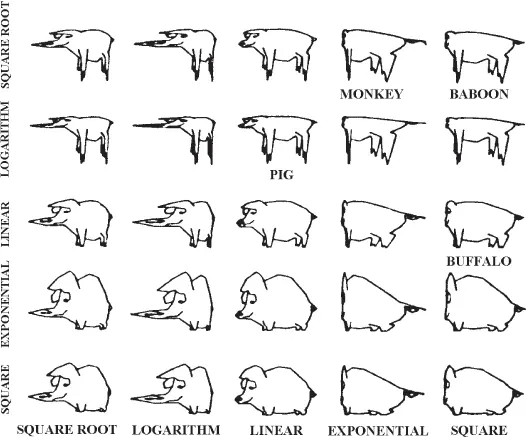
Рис. 6. Геометрическая интерпретация феноменологических изменений [Barger, 1974].

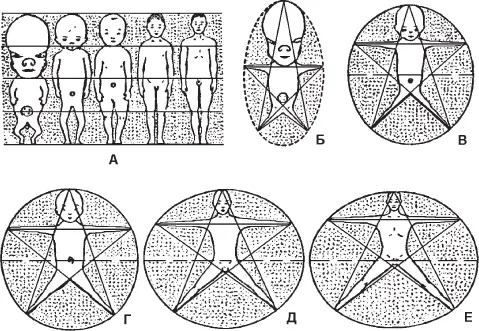
Рис. 7. Онтогенетические изменения человеческого тела в позе прямостояния ( а ) и распластанной позе ( б – е ); слева направо: ( а) – двухмесячный эмбрион, четырехмесячный эмбрион, новорожденный, 6-ти и 25-летний человек (из книги Б.М. Пэттеи «Эмбриология человека». М.: Медгиз, 1959); ( б ) – двухмесячный эмбрион, ( в) – четырехмесячный эмбрион, ( г ) – новорожденный, ( д ) – шестилетний человек, (е) – 25-летний человек [Петухов, 1981, с. 120].

Вернемся теперь к тем нашим проблемам, которые порождены обращением биологов к компьютерному анализу многомерных данных. Здесь со всей серьезностью возникают вопросы:

Как организовано собственно биологическое пространство, т. е. какова его метрика? Обращаясь к многомерному анализу данных, можно ли опираться на некоторую единую, биологически обоснованную метрическую организацию пространства, или мы должны без конца варьировать выбором метрики, опираясь на эвристику?

Каким преобразованиям должны подвергаться переменные? Нужно ли обращаться к сопряженным преобразованиям переменных, скажем, имея дело с численностью и биомассой, переходить к их отношению или к извлечению корня квадратного из их произведения? Уместно ли обращаться к χ 2 метрике? Разумно ли переходить от непосредственно измеряемых переменных х i, х jк параметрам, связывающим их формулой аллометрического роста:

х i = ах j b .

Параметры a и b мы можем рассматривать как новые косвенно изменяемые величины. Они, кажется, имеют все же четкую биологическую интерпретацию [93]. Здесь может быть поставлен и такой вопрос: как может быть геометризировано собственно биологическое время и какова его связь с астрономическим временем? Это новые для биологов проблемы. В плане общетеоретическом они могут рассматриваться как прямое следствие представления эволюционизма в терминах силлогизма Бейеса. Но в плане практическом – и об этом не надо забывать – они возникли в результате соприкосновения биологической науки с компьютерной техникой. И со всей серьезностью нужно подчеркнуть, что если поставленные здесь проблемы не будут решены, если природа биопространства не будет осмыслена, то обращение биолога к компьютеру будет выдавать произвольные, не содержательные результаты. Интересно обратить внимание на то, что здесь мы впервые подходим к философски звучащему вопросу о роли наблюдателя в биологическом исследовании. Оказывается, что биологическое пространство – это та новая биологическая реальность, которая не существует сама по себе, она появляется только в результате взаимодействия исследователя с природой. Здесь возникает некоторая, хотя, может быть, и отдаленная параллель с представлением о роли наблюдателя в современной физике.

Наш метрический подход к геометризации биологии можно, в плане историческом, противопоставить хорошо известному подходу Н. Рашевского [94]. Рассматривая возможность построения теоретической биологии как абстрактной дисциплины, он обращается к топологии, полагая, что в живой природе, в отличие от неживой, характерной чертой организации являются не метрические отношения, а непрерывные преобразования объектов друг в друга [Rashevsky, 1954]:

В то время как физические феномены являются манифестацией метрических свойств четырехмерного универсума, биологические феномены, возможно, способны отражать некоторые локальные топологические свойства этого универсума (с. 317).

Топологические пространства или комплексы, которыми представлены различные организмы, все получены из одного или лишь немногих изначальных пространств или комплексов путем одной и той же трансформации, содержащей один или более параметров, разным значениям которых соответствуют различные организмы (с. 325).