ВП СССР - Краткий курс...

Если эту процедуру последовательно проделать для каждой отрасли из множества выделенных во многоотраслевой производственно-потреби­тель­ской системе, то получится квадратная таблица (матрица) обмена продукцией отраслями между собой в процессе их производства, вокруг которой разполагаются ещё несколько строк и столбцов, харак­те­ри­зующих внепроизводственное потребление и разные аспекты упра­в­ления макро- и микроэкономикой. Эта таблица, включая и окружа­ющие её дополнительные столбцы и строки внепроизводственных характе­ристик, представляет собой одну из форм представления межотраслевого баланса. Баланс может быть представлен в натуральном и финансовом учёте продукции.

Математически баланс может быть описан системой линейных уравнений, повторяющих упорядоченность по строкам и столбцам упомянутой таблицы продуктообме­на отраслей:

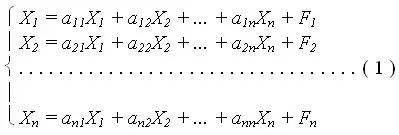
Здесь Х 1, ... , X n — валовый выпуск отраслей с первой по n -ную. Правая часть каждого из уравнений характе­ри­зует разпределение продукции соответствующей отрасли между её потребителями:

1. Всем набором отраслей в сфере производства (блок 18 РСП на рис. 4) — столбцы, содержащие Х 1, ... , X n ; каждый член i- тогоуравнения вида а ijХ j представляет собой объём поставок продукции отрасли i для обеспечения производства в отрасли j в объёме X j . Иначе говоря, представленная модель — линейная и предполагает, что потребности каждой отрасли в продукции других отраслей пропорцио­нальны объёму выпуска ею продукции.

2. Продукцией конечного потребления — столбец F 1, ... ,F n .

В этой системе второй коэффициент первого урав­нения — а 12 — численно равен количеству продукта, производимого от­раслью № 1, необходимого отрасли № 2 для производ­ства единицы учёта продукции отрасли № 2. Все осталь­ные коэффициенты а 11 , а 12 , ... , а nn имеют такой же смысл, конкретно определяемый их положением в системе уравнений, и на­зываются коэффициентами прямых затрат . Каждый из них характеризует культуру производства отрасли-потребителя: сколько необходимо продукции отрасли-по­ставщика по технологии + сколько будет украдено + сколько будет утрачено по бесхозяйственности.

В совокупности коэффициенты прямых затрат обра­зуют квадратную таблицу — матрицу A , если говорить языком математики.

Здесь и далее:

· матрицы обозначены заглавными буквами, набранными жирным курсивным шрифтом: А , А T, Е , F , Х .

· элементы матриц обозначены теми же буквами, что и матрицы: либо строчными, либо заглавными, но набранными курсивным нежирным шрифтом, с индексами, указующими положение в матрице: a 12 , a ij , a nn ; некоторые матрицы обозначены через их элементы, помещенные в квадратные скобки, например: [P Б ii -1] , A=[a ij] .

· вектора обозначены заглавными и строчными буквами, набранными курсивным нежирным шрифтом, при которых могут быть мнемонические индексы определяющие дополнительную смысловую нагрузку, смысл которой поясняется в тексте: Х , r , r ЗСТ , X K .

· компоненты векторов обозначены также как и сами вектора, но в сочетании с индексами-нумераторами компонент, как числен­ны­ми, так и буквенными: r ЗСТ 1 j , X 1, X i , X K j .

Баланс может быть составлен раздельно по демогра­фически обусловленному спектру и по деградационно-паразитическому спектру; может быть составлен и объединенный баланс. В баланс продуктообмена в форме (1) может быть включен и экспортно-импортный обмен разсматриваемой многоотраслевой системы с другими производственно-потребительскими системами.

Уравнения межотраслево­го баланса продуктообмена могут быть записаны в матрично-векторной форме:

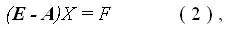
где: E — диагональная матрица [28], т.е. все эле­менты которой — нули, кроме e 11= e 22= ... = e nn= 1, X и F — векторы-столбцы, спектры производства, вбираю­щие в себя Х 1, ... , X n и F 1, ... , F n , соответственно. Уравне­ние (2) позволяет ответить на вопрос: каким должен быть спектр валовых мощностей X при культу­ре производ­ства, описываемой матрицей A , чтобы получить спектр конечной продукции F .

Если каждое уравнение в натуральном балансе ум­ножить почленно на цену продукта (спектра производ­ства отрасли в целом), производимого отраслью, соответствующей уравнению, то каждая строка системы (1) характеризует източники доходов этой отрасли от продажи ею продукции; а столбец, соответствующий номеру отрасли, характеризует её расходы по оплате продукции, приобретаемой ею у поставщиков в обеспечение её собственного производ­ства.

После этого ниже системы уравнений можно выпи­сать ещё несколько строк функционально обусловленных расходов , производимых отраслью помимо оплаты продукции её поставщиков в процессе её собственного производства:

· Фонд заработной платы.

· Фонд развития и реконструкции производства.

· Финансирование совместных (с предприятиями других отраслей) программ.

· Благотворительность.

· Свободные, неразпределённые средства.

· Кредитный и страховой баланс (сальдо).

· Баланс налогов и дотаций (сальдо).

Эти записи помещаются ниже строк баланса продук­тообмена в столбцах соответствующих отраслей. Так межотраслевой баланс переводится в стоимостную форму учёта продукции. При стоимостном учёте возможны балансовые уравнения иного рода:

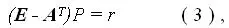
где матрица A Т получена в результате транспониро­вания матрицы A (транспонирование — запись в столбец строки матрицы A с тем же номером, то есть a 12 Т= a 21 и т.д.); здесь и далее верхний индекс « Т » — знак транспонирования матриц (по отношению к веторам-столбцам он эквивалентен записи их в виде строки; а по отношению к строкам — записи их в виде столбцов при сохранении порядка следования их компонент слева направо и сверху вниз соответственно). P — вектор цен на продук­цию, учитываемую в балансе продуктообмена отраслей; а r — вектор-столбец, для каждой отрасли соответствующая компонента которого — вся совокупность ранее пере­численных функционально обусловленных расходов за изключением закупок продукции у поставщиков, уже описанной мат­ри­цей A , отнесенных к единице учёта валового выпуска отрасли. Компо­ненты вектора r традиционно называют «долями добавленной стоимости» в составе цены продукции (це­ны единицы учёта продукции). Само уравнение (3) называют урав­нением равновесных цен. Оно описывает характе­ри­стики рентабельности отраслей в целом во всём их множестве при спектре валового производства X , культу­ре производства, описываемой матрицей A , ценах, сведенных в вектор-столбец P и кредитно-финансовой политике, описываемой составля­ющими вектора-столбца r .