ВП СССР - Краткий курс...

5. Критерий оптимального выбора последовательности шаговых управлений U n и соответствующей траектории в пространстве формальных параметров имеет вид:

V = V 0 (X 0 , U 0) + V 1 (X 1 , U 1) + ...+ V N - 1 (X N- 1 , U N - 1) + V N (X N) .

Критерий V принято называть полным выигрышем, а входящие в него слагаемые — шаговыми выигрышами . В задаче требуется найти последовательность шаговых управлений U n и траекторию, которым соответствует максимальный из возможных полных выигрышей . По своему существу полный “выигрыш” V — мера качества управления процессом в целом . Шаговые выигрыши, хотя и входят в меру качества управления процессом в целом, но в общем случае не являются мерами качества управления на соответствующих им шагах, поскольку метод предназначен для оптимизации управления процессом в целом, а эффектные шаговые управления с большим шаговым выигрышем, но лежащее вне оптимальной траектории интереса не представляют. Структура метода не запрещает при необходимости на каждом шаге употреблять критерий определения шагового выигрыша V n , отличный от критериев, принятых на других шагах.

С индексом n — указателем-определителем множеств возможных векторов состояния — в реальных задачах может быть связан некий изменяющийся параметр, например: время, пройденный путь, уровень мощности, мера расходования некоего ресурса и т.п. То есть метод применим не только для оптимизации управления процессами, длящимися во времени, но и к задачам оптимизации многовариантного одномоментного или нечувствительного ко времени решения, если такого рода “безвременные”, “непро­цес­сные” задачи допускают их многошаговую интерпретацию.

Теперь обратимся к рис. 6 — рис. 8, повторяющим взаимно связанные рис. 40, 41, 42 из курса теории автоматического управления П. де Ла Барьера.

На рис. 6 показаны начальное состояние системы «0» и множества её возможных последующих состояний «1», «2», «3», а также возможные переходы из каждого возможного состояния в другие возможные состояния.

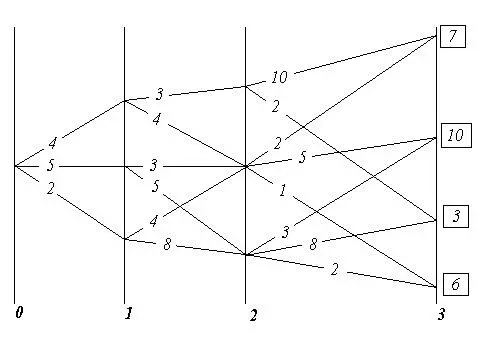
И всё это вместе похоже на карту настольной детской игры, по которой перемещаются фишки: каждому переходу-шагу соответствует свой шаговый выигрыш, а в завершающем процесс третьем множестве — каждому из состояний системы придана его оценка, помещенная в прямоугольнике. Принципиальное отличие от игры в том, что гадание о выборе пути, употребляемое в детской игре, на основе бросания костей или вращения волчка и т.п., в реальном управлении недопустимо, поскольку это — передача целесообразного управления тем силам, которые способны управлять выпадением костей, вращением волчка и т.п.

Если выбирать оптимальное управление на первом шаге, то необходимо предвидеть все его последствия на последующих шагах. Поэтому описание алгоритма метода динамического програм­мирования часто начинают с описания выбора управления на последнем шаге, ведущем в одно из завершающих процесс состояний. При этом ссылаются на «педаго­ги­ческую практику», которая свидетельствует, что аргументация при опи­сании алгоритма от завершающего состояния к начальному состоянию легче возпринимается, поскольку опирается на как бы уже сложившиеся к началу разсматриваемого шага условия, в то время как возможные завершения процесса также определены.

В соответствии с этим на рис. 7 анализируются возможные переходы в заверша­ю­щее множество сос­тояний «3» из каж­дого возможного сос­то­яния в ему пред­ше­ствующем множестве состояний «2», будто бы весь предшеству­ю­щий путь уже прой­ден и осталось пос­ледним выбором оп­ти­ма­льного шагового управления завер­шить весь процесс. При этом для каждого из состояний в мно­жестве «2» определяются все полные выигрыши как сумма = «оценка перехода» + «оценка завершающего состояния». Во множестве «2» из полученных для каждого из состояний, в нём возможных полных выигрышей, определяется и запоминается максимальный полный выигрыш и соответствующий ему переход (фрагмент траектории). Максимальный полный выигрыш для каждого из состояний во множестве «2» взят в прямоугольную рамку, а соответствующий ему переход отмечен стрелкой. Таких оптимальных переходов из одного состояния в другие, которым соответствует одно и то же значение полного выигрыша, в принципе может оказаться и несколько. В этом случае все они в методе неразличимы и эквивалентны один другому в смысле построенного критерия оптимальности выбора траектории в пространстве параметров, которыми описывается система.

После этого множество «2», предшествовавшее завершающему процесс множеству «3», можно разсматривать в качестве завершающего, поскольку известны оценки каждого из его возможных состояний (максимальные полные выигрыши) и дальнейшая оптимизация последовательности шаговых управлений и выбор оптимальной траектории могут быть проведены только на ещё не разсмотренных множествах, предшествующих множеству «2» в оптимизируемом процессе (т.е. на множествах «0» и «1»).

Таким образом, процедура, иллюстрируемая рис. 7, работоспособна на каждом алгоритмическом шаге метода при переходах из n -го в (n - 1) -е множество, начиная с завершающего N ‑ного множества до начального состояния системы.

В результате последовательного попарного перебора множеств, при прохождении всего их набора, определяется оптимальная последовательность преемственных шаговых управлений, максимально возможный полный выигрыш и соответствующая им траектория. На рис. 8 утолщённой линией показана оптимальная траектория для разсматривавшегося примера.

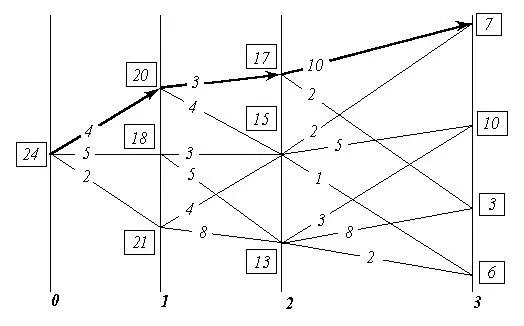
В разсмотренном примере критерий оптимальности — сумма шаговых выигрышей. Но критерий оптимальности может быть построен и как произведение обязательно неотрицательных сомножителей.

Поскольку результат (сумма или произведение) не изменяется при изменении порядка операций со слагаемыми или сомножителями, то алгоритм работоспособен и при переборе множеств возможных состояний в порядке, обратном разсмотренному: т.е. от исходного к завершающему множеству возможных состояний.

Если множества возможных состояний упорядочены в хронологической последовательности, то это означает, что расчётная схема может быть построена как из реального настоящего в прогнозируемое определённое будущее, так и из прогнозируемого опре­делённого будущего в реальное настоящее. Это обстоятельство говорит о двух неформальных соотношениях реальной жизни, лежащих вне алгоритма: