Яков Перельман - Квадратура круга

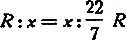
откуда

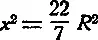
т. е. площадь квадрата со стороною х приближенно равна площади круга.

Чем точнее известно значение π, тем, очевидно, точнее может быть выполнено такое построение. Естественно поэтому, что позднейшие работы математиков над квадратурой круга были тесно связаны с получением возможно более точного π. В течение почти двух тысячелетий после Архимеда нахождение π велось по методу великого математика древности; способ Архимеда заключался в том, что площадь круга сравнивалась с площадями вписанных и описанных правильных многоугольников, число сторон которых последовательно удваивается. Совершенствуя метод Архимеда, позднейшие математики получали для π все более и более точные значения. Представленное в виде десятичных дробей, значение π выражалось десятками цифр. Так, голландский математик Лудольф ван-Цейлен, пользуясь методом Архимеда, вычислил (в 1615 г.) π c 31 верным десятичным знаком: π=3.1415926535897932384626433832795. (Эта дробь называется «Лудольфовым числом»). Оставалось, однако, неизвестным, имеет ли этот все удлиняющийся ряд цифр конец, или же он бесконечен.

Когда, во второй половине XVII века, открыто было исчисление бесконечно малых, эта отрасль высшей математики нашла более быстрые и удобные приемы вычисления π нежели те, которыми располагает элементарная математика. Открыты были весьма важные для теории соотношения между числом π и другими математическими величинами. Наконец, выявлены были замечательные особенности числа π, бросившие новый свет на старинную задачу о квадратуре круга.

До настоящего времени известно 707 цифр в числе π. Они были вычислены в 1874 г. английским математиком Шенксом. Это «самое длинное π» изображено под потолком зала математических развлечений Дома Занимательной Науки в Ленинграде, вдоль четырех стен помещения.

Каким бы путем ни приступать к задаче о квадратуре круга, она приводит к необходимости построить отрезок x , удовлетворяющий уравнению

иначе говоря, задача приводит к построению формулы 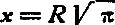. Чтобы установить, выполнимо ли это построение, нужно выяснить, какие вообще выражения могут быть построены циркулем и линейкой. В высшей математике (в той ее отрасли, которая называется аналитической геометрией) доказывается, что циркулем и линейкой могут быть построены только такие выражения, в состав которых входят действия сложения, вычитания, умножения, деления, извлечения квадратного корня и никакие другие; при этом число перечисленных операций не должно быть бесконечно велико. Тем же условиям должны удовлетворять и числа, входящие в формулу: если они но даны прямо, они должны получаться в результате только перечисленных действий.

Так, например, следующая формула

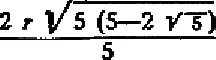
может быть построена (это — сторона правильного описанного десятиугольника). Напротив, простая на вид формула удвоения куба

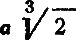
не может быть построена.

Обращаясь к формуле квадратуры круга, 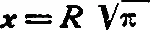, мы видим, что она заключает только действия умножения и извлечения квадратного корня, т. е. операции, позволяющие выполнить построение. Однако, в формулу входит число π, и надо установить, допускает ли формула, содержащая это число, выполнение построения. Немецкий математик Ламберт доказал в 1766 г., что число π принадлежит к роду чисел, называемых несоизмеримыми (или иррациональными); такие числа не могут быть точно выражены конечным рядом цифр. Среди не-математиков распространено мнение, что неразрешимость квадратуры круга обусловлена несоизмеримостью числа π, так как нельзя будто бы построить число, выражающееся бесконечным рядом цифр. Это обоснование неправильно. Существует такой род несоизмеримых чисел, которые могут быть построены. 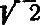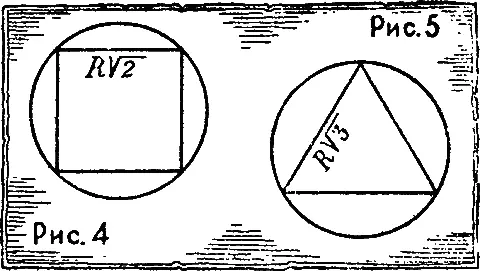В качестве примеров укажем числа и 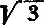; они выражаются десятичными дробями с бесконечным рядом цифр после запятой, и тем не менее их легко построить: первое — как сторону вписанного квадрата (рис. 4), второе — как сторону вписанного равностороннего треугольника (рис. 5).

Вообще, все те числа, которые получаются путем однократного или повторного (но не бесконечного) извлечения квадратного корня, могут быть строго геометрически построены.

К этому роду несоизмеримых чисел π не принадлежит. В 1882 г. немецкий математик Линдеман опубликовал исследование, из которого вытекает, что число π не может быть получено в результате конечного ряда извлечений квадратного корня. Теи самым устанавливается невозможность построения формулы квадратуры круга, а следовательно, и неразрешимость этой задачи.

Доказательство неразрешимости какой-либо задачи рассматривается в математике как своего рода решение проблемы, потому что такое утверждение дает вполне исчерпывающий ответ на поставленный вопрос. В этом смысле доказательство Линдемана можно считать решением задачи о квадратуре круга, решением, полагающим конец двухтысячелетней работе над этой проблемой. Продолжают искать другого решения задачи только малосведущие любители. «Таких искателей — писал еще в 18-м столетии математик Ламберт — всегда будет достаточно, и если судить о будущих по их предшественникам, то это будут по большей части люди, мало смыслящие в геометрии и лишенные возможности правильно оценивать свои силы. Там, где им не хватает знания и понимания, где они не могут ничего сделать c помощью правильных последовательных выводов, там жажда славы и денег создает софизмы, которые чаще всего не отличаются ни особой тонкостью, ни особой замысловатостью».

Остается рассмотреть еще вопрос: нужно ли точное решение квадратуры круга для фактических расчетов? Оказывается, надобности в точном решении этой задачи никогда практически не возникает. Достаточно располагать таким решением, которое давало бы приближенный результат с желаемой степенью точности; а этого можно достичь, пользуясь даже частью известных уже цифр в выражении π.