Довид Ласерна - На волне Вселенной. Шрёдингер. Квантовые парадоксы

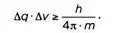
Неравенство показывает, что граница неопределенности для q и v зависит от отношения между постоянной Планка и массой т. Более того, для макроскопических объектов h будет незначительной, следовательно, Δq и Δρ тоже могут иметь малые значения. Таким образом, создается впечатление, что мы можем определить результат с желаемой точностью. Но с того момента как масса и размер приближаются к постоянной Планка, неопределенности начинают выходить на первый план. Чтобы доказать это, применим отношения неопределенности к трем различным объектам.

1. Автомобиль. Примем его массу примерно равной одной тонне:

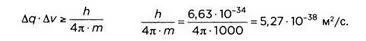
Предположим, что автомобиль перемещается со скоростью 100 км/час (около 30 м/сек):

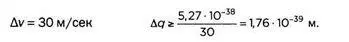
Разница между размером машины, который измеряется в метрах, и неопределенностью положения равна единице с 39 нулями перед ней. Невообразимо мало.

2. Пчела массой ОД грамма:

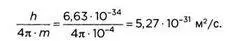
Это насекомое может перемещаться с максимальной скоростью 7 м/с:

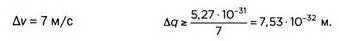
Для пчелы длиной несколько сантиметров масштаб разницы между неопределенностью ее положения и размером — 10~ 30. Это очень мало.

3. Электрон массой около 9,11 х 10 -31кг:

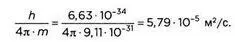
Присвоим электрону среднюю скорость 10 6м/сек, или примерно 1% от скорости света:

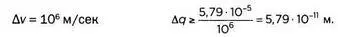
Радиус орбиты электрона водорода в фундаментальном состоянии (модель Бора), как правило, является величиной, лежащей в основе модели атома. Как мы уже увидели, радиус соответствует волновой функции Шрёдингера для той же энергии. Его значение r = 5,29 х 10 -11метров. Таким образом, в случае с электроном, неопределенность его положения — одного порядка с размером места, в котором он находится: невозможно его отследить.

Мы рассмотрели конкретный случай, но подобная неопределенность может наблюдаться в любом экспериментальном контексте. Физики обозначают степень неопределенности измерения с помощью символа Δ. Таким образом, Δx = 0 означает, что пространственная координатах частицы может иметь лишь одно значение, то есть положение частицы четко зафиксировано. Однако Δx = 5 означает, что частица может находиться где угодно в радиусе 5 метров. Гейзенберг не был удовлетворен изучением неопределенности и определил ее границы при помощи постоянной Планка:

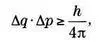
где q означает положение частицы, а р — ее импульс. Речь идет о принципе неопределенности, в котором объединены две различные физики, и наше знание об одной обнаруживается через информированность о другой.

Помимо импульса и положения, Гейзенберг присвоил свое соотношение неопределенности другим парам сопряженных величин, произведение которых измеряется в тех же единицах, что и действие, то есть, подобно постоянной Планка, определяется как произведение энергии на время:

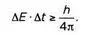
М, L и Т— фундаментальные физические величины (масса, длина и время). Считается, что произведение времени на энергию выражается в тех же единицах, что и произведение длины на импульс, а также постоянная Планка:

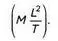
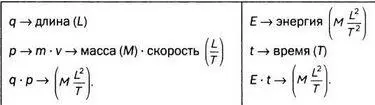
Гейзенберг сделал следующий вывод: «Чем точнее определено положение, тем меньше мы можем сказать в этот момент об импульсе, и наоборот». Предложенное им уравнение позволяет играть с этими нечеткостями. Как только какое-либо значение присваивается Δq, Δр вынуждено соответствовать условию:

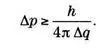
Когда Δq стремится к нулю, знаменатель очень быстро уменьшается, что устремляет Δр в бесконечность. Знать точное положение — игнорировать все, что касается импульса. На макроскопическом уровне, где h невозможно обнаружить, уравнение вводит нас в привычную ситуацию, когда q и р определены одновременно с желаемой точностью:

h → 0; Δq • Δp => 0; сравнимо с Δq - Δр - 0.

Принцип неопределенности Гейзенберга работает как качели, на которых то взмывают вверх, то опускаются «ниже уровня радара» волновые и корпускулярные свойства квантовых сущностей. Чем сильнее Aq уменьшается, тем лучше мы можем наблюдать частицы. Напротив, уменьшение р отправляет нас к волне, положение которой не может быть определено, но ее скорость v — четко определена (см. рисунок). Таким образом, каждый из элементов квантового мира меняется исходя из того, откуда на него устремлен взгляд наблюдателя.

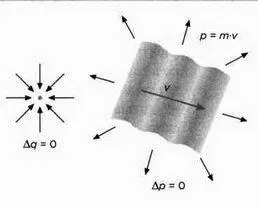
Некоторые физики решили, что принцип неопределенности ставит под сомнение их квалификацию экспериментаторов, и принялись ставить опыты, определяющие положение и импульс, нарушая при этом установленные ограничения. Выдвинул свои аргументы против такого субъективного аспекта квантовой теории и Эйнштейн.

Однако все возражения потерпели неудачу.

Чтобы вычислить траекторию объекта, необходимо знать всего лишь две его характеристики: положение в определенный момент и импульс, указывающий направление, в котором объект перемещается. Отношения неопределенностей не связаны с траекториями и, таким образом, помогают воплотить давнюю мечту Гейзенберга, которая появилась у него еще на Гельголанде. Тогда физик предупреждал: «Я все силы отдам уничтожению понятия орбиты». Такая решимость пугала Эйнштейна, общая теория относительности которого основывалась на расчете траекторий в пространстве, в четырех измерениях. Но идеи Гейзенберга угрожали не только траекториям. В своей статье от 1927 года ученый пришел к выводу: «На самом деле, однако, в жесткой формулировке закона причинности, гласящей: «Если мы точно знаем настоящее, мы можем вычислить будущее», ложной является не вторая часть, а предпосылка. Мы принципиально не можем узнать настоящее во всех деталях». Это незнание подрывает нашу способность к предвидению. Разрыв связи между настоящим и ближайшим будущем, вычисленным благодаря знанию и положения, и импульса, повлек крах классической физики. Конечно, эта невозможность существовала в науке и ранее. Она ощущалась во всех теориях, касавшихся как атомов и молекул, так и определения положения и импульса мириада классических объектов. Однако этот провал закона причинности связан с человеческим несовершенством, а не с действием объективного природного механизма.