Виктор Стенджер - Бог и Мультивселенная. Расширенное понятие космоса

Это так называемое медленное вращение — необходимая черта большинства инфляционных моделей, которую искусственным образом внедрили в новые инфляционные модели, упомянутые ранее. Хаотической модели она присуща изначально. Медленное вращение обеспечивает промежуток времени, достаточный для того, чтобы центр кристаллизации расширился на много порядков, прежде чем шарик наконец достигнет дна. Оказавшись на дне, он начинает кататься из стороны в сторону со все более сужающейся амплитудой, уже больше не останавливаясь до конца. Из энергии, расходуемой на трение, образуются элементарные частицы, которые затем формируют Вселенную.

Все это можно выразить количественно хотя бы просто для наглядности. Для инфлятонного поля φ можно записать плотность потенциальной энергии как формулу гармонического осциллятора u(φ) = m 2φ 2/2, где m — масса кванта этого поля, который можно считать частицей, называемой инфлятоном. Значение т неизвестно, и потому эта величина считается переменным параметром, в этой модели он такой один. Теперь, если мы подставим и в уравнение движения, то сможем использовать численные методы для расчета значений φ, H и космологического масштабного фактора a в зависимости от времени. В моей книге «Постижимый космос» (Comprehensible Cosmos) все это детально разбирается, включая математические выводы всех уравнений на доступном студентам уровне {254} 254 Stenger Victor J. The Comprehensible Cosmos: Where Do the Laws of Physics Come From? — Amherst, N. Y.: Prometheus Books, 2006. . Здесь я привожу только результаты.

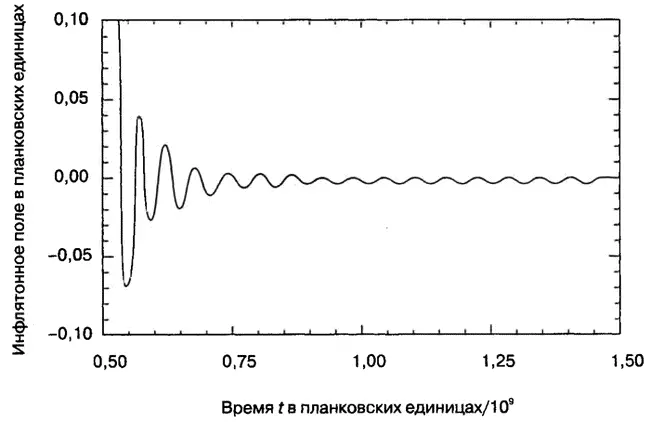
Работать мы будем в планковских единицах, где ħ = h/2π = с = G = 1 (G — это гравитационная постоянная Ньютона). Для наглядности я выбрал значение начальной флуктуации в поле φ, равное 10 планковским единицам, и m = 10 -7планковских единиц (10 11ГэВ). На рис. 12.3 показано движение шарика, катящегося вниз по склону из этой точки. По мере того как шарик медленно спускается, объем Вселенной увеличивается экспоненциально. Его движение замедляется расширением пространства, поэтому шарик теряет свою энергию по мере того, как он катится вниз и затем колеблется из стороны в сторону в области нижних значений своей потенциальной энергии с уменьшающейся амплитудой.

На рис. 12.4 изображено, как изменяется поле со временем t в единицах планковского времени. Область графика с t < 0,5 не показана, чтобы продемонстрировать затухающие колебания поля. За период времени t < 0,6, поле уменьшается с 10 единиц (не показано на графике) до нуля и затем колеблется в области нуля с все более уменьшающейся амплитудой.

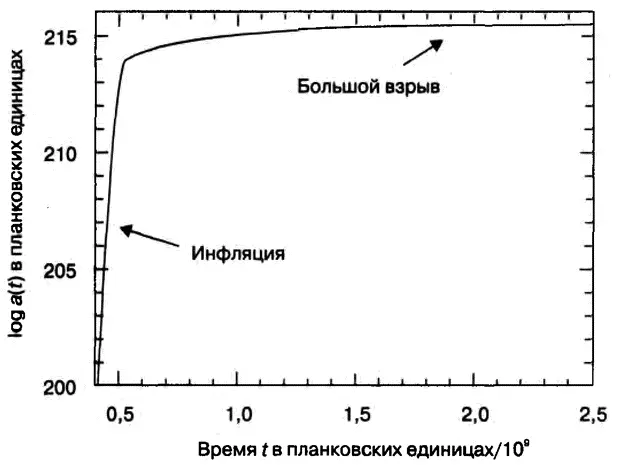
На рис. 12.5 показано изменение масштабного фактора Вселенной а, который для наших целей можно принять за радиус Вселенной. Вслед за экспоненциальной инфляцией Вселенной, во время которой она увеличилась на 214 порядков, наступает плавный переход к привычному хаббловскому расширению. Это просто наглядное изображение, которое не претендует на точное моделирование нашей Вселенной.

В 1980-е годы, пока специалисты по астрофизике частиц носились с невероятной идеей о том, что Вселённая увеличилась на множество порядков в течение первой мельчайшей доли секунды, астрономы-наблюдатели делали свои открытия: то, что находили в космосе их новые телескопы, оказалось невероятным.

В 70-е годы XX века Вселенную в общем виде представляли в форме более или менее однородного распределения скоплений галактик, движущихся друг от друга по единому принципу вследствие расширения Вселенной по закону Хаббла. Но к началу 1980-х начали накапливаться данные, свидетельствующие о том, что тысячи галактик в области пространства, равной миллионам световых лет, проявляют небольшие, но поддающиеся измерению отклонения от лучевой скорости разбегания, которую, как ожидалось, придает им расширение Вселенной. Движение галактик в нашем местном скоплении, похоже, направлено в сторону области, которая находится примерно в 200 млн. световых лет от нас, в центре сверхскопления Гидры — Центавра. Эта точка получила название Великий аттрактор {255} 255 Dressier Alan Michael. Voyage to the Great Attractor: Exploring Intergalactic Space. — New York: A. A. Knopf, 1994. .

В течение нескольких лет в распределении скоплений, сверхскоплений (скоплений скоплений) и комплексов сверхскоплений были обнаружены другие неожиданные структуры. В 1987 году мой коллега по Гавайскому университету Брент Талли наблюдал нитевидную структуру длиной 1 млрд. световых лет и шириной 150 млн. световых лет, которую он назвал комплексом сверхскоплений Рыб — Кита. Он состоит из пяти сверхскоплений общей массой в 10 18раз больше массы Солнца, включая сверхскопление Девы, масса которого равна 10 15солнечным массам, частью которого мы являемся.

Как мы уже знаем: измерение расстояний всегда было серьезным испытанием для астрономов. Они разработали так называемую лестницу космических расстояний. Она представляет собой набор методов, каждый из которых применяется до некоторого предельного расстояния, после чего вступает в силу следующий. Методы в достаточной степени перекрывают друг друга, так что с помощью одного из них можно уточнить показания, полученные с помощью другого.

Не думаю, что стоит подробнее описывать эти методы. Я уже рассказал вам о способе определения расстояний по параллаксу, который используется для звезд, расположенных близко — на расстоянии до сотни световых лет, и об определении расстояний по цефеидам, что работает для галактик, расположенных на расстоянии до 13 млн. световых лет от Земли. В 1977 году Талли в соавторстве с Ричардом Фишером опубликовал новый метод определения расстояний до спиральных галактик, который заключается в определении зависимости между внутренней светимостью галактики и скоростью ее вращения {256} 256 Tully R. Brent and Fisher J. Richard. A New Method of Determining Distances to Galaxies //Astronomy and Astrophysics, 54,1977: 661–673. . Как и в случае с другими методами, вы определяете расстояние, измеряя наблюдаемую на Земле светимость, и предполагаете, что она падает до наблюдаемого значения пропорционально квадрату расстояния до объекта. С помощью этого и других методов Талли и Фишер создали атлас галактик, названных ими близкими {257} 257 Tully R. Brent and Fisher J. Richard. Nearby Galaxies Atlas. — Cambridge; New York: Cambridge University Press, 1987. .