Феликс Зигель - Астрономы наблюдают

Самый древний из них гномон (рис. 1). В простейшем варианте он представляет собой вертикальный стержень, отбрасывающий тень на горизонтальную плоскость. Зная длину гномона L и измерив длину I отбрасываемой им тени, можно найти угловую высоту h Солнца над горизонтом по современной формуле:

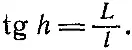
Древние использовали гномоны для измерения полуденной высоты Солнца в различные дни года, а главное в дни солнцестояний, когда эта высота достигает экстремальных значений. Пусть полуденная высота Солнца в день летнего солнцестояния равна Н, а в день зимнего солнцестояния h. Тогда угол ε между небесным экватором и эклиптикой равен

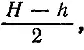
а наклон плоскости небесного экватора к горизонту, равный 90°—φ, где φ — широта места наблюдения, вычисляется по формуле

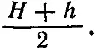
С другой стороны, внимательно следя за длиной полуденной тени, можно достаточно точно подметить, когда она становится самой длинной или самой короткой, то есть иначе говоря, зафиксировать дни солнцестояний, а значит, и продолжительность года. Отсюда легко вычислить и даты солнцестояний.

Таким образом, несмотря на простоту, гномон позволяет измерять очень важные в астрономии величины. Эти измерения будут тем точнее, чем крупнее гномон и чем, следовательно, длиннее (при прочих равных условиях) отбрасываемая им тень. Так как конец тени, отбрасываемой гномоном, не бывает резко очерчен (из-за полутени), то на некоторых древних гномонах сверху укрепляли вертикальную пластинку с маленьким круглым отверстием. Солнечные лучи, пройдя сквозь это отверстие, создавали четкий солнечный блик на горизонтальной плоскости, от которого измеряли расстояние до основания гномона.

Еще за тысячу лет до нашей эры в Египте был построен гномон в виде обелиска высотой в 117 римских футов. В царствование императора Августа гномон перевезли в Рим, установили на Марсовом поле и определяли с его помощью момент полдня. На Пекинской обсерватории в XIII веке н. э. был установлен гномон высотой 13 м, а знаменитый узбекский астроном Улугбек (XV век) пользовался гномоном, по некоторым сведениям, высотой 55 м. Самый же высокий гномон работал в XV веке на куполе Флорентийского собора. Вместе со зданием собора его высота достигала 90 м.

К числу древнейших угломерных инструментов принадлежит также астрономический посох (рис. 2).

Вдоль градуированной линейки АВ перемещалась подвижная рейка CD, на концах которой иногда укрепляли небольшие стержни — визиры. В некоторых случаях визир с отверстием был и на том конце линейки АВ, к которому наблюдатель прикладывал свой глаз (точка А). По положению подвижной рейки относительно глаза наблюдателя можно было судить о высоте светила над горизонтом, или об угле между направлениями на две звезды.

Древние греческие астрономы пользовались так называемым трикветром, состоящим из трех соединенных вместе линеек (рис. 2). К вертикальной неподвижной линейке АВ на шарнирах прикреплены линейки ВС и АС. На первой из них укреплены два визира или диоптра m и п. Наблюдатель направляет линейку ВС на звезду так, чтобы звезда одновременно была видна сквозь оба диоптра. Затем, удерживая линейку ВС в этом положении, к ней прикладывают линейку АС таким образом, чтобы расстояния ВА и ВС были равны между собой. Это было легко сделать, так как на всех трех линейках, составляющий трикветр, имелись деления одинаковой шкалы. Измерив по этой шкале длину хорды АС, наблюдатель затем по специальным таблицам находил угол ABC, то есть зенитное расстояние звезды.

И астрономический посох и трикветр не могли обеспечить высокую точность измерений, и потому им нередко предпочитали квадранты — угломерные инструменты, достигшие к концу средневековья высокой степени совершенства. В простейшем варианте (рис. 3) квадрант представляет собой плоскую доску в форме четверти градуированного круга. Около центра с этого круга вращается подвижная линейка с двумя диоптрами (иногда линейку заменяли трубкой). Если плоскость квадранта вертикальна, то по положению трубы или визирной линейки, направленных на светило, легко измерить высоту светила над горизонтом. В тех случаях, когда вместо четверти круга использовали его шестую часть, инструмент назывался секстантом, а если восьмую часть — октантом. Как и в других случаях, чем крупнее был квадрант или секстант, чем точнее была его градуировка и установка в вертикальной плоскости, тем более точные измерения с ним можно было выполнять. Для обеспечения устойчивости и прочности крупные квадранты укрепляли на вертикальных стенах. Такие стенные квадранты еще в XVIII веке считались лучшими угломерными инструментами.

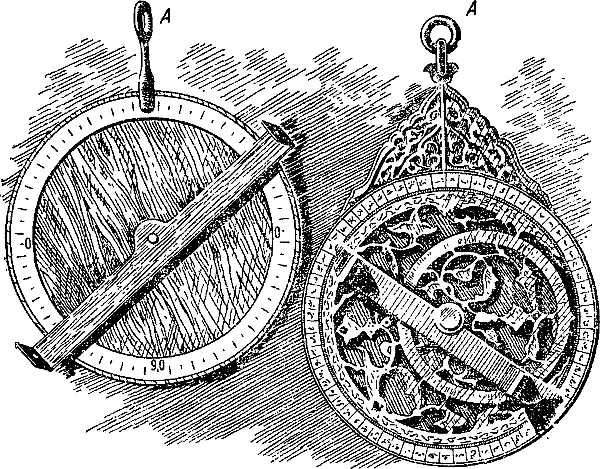
К тому же типу инструментов, что и квадрант, относится астролябия или астрономическое кольцо (рис. 4). Разделенный на градусы металлический круг подвешивается к какой-нибудь опоре за кольцо А. В центре астролябии укреплена алидада — вращающаяся линейка с двумя диоптрами. По положению алидады, направленной на светило, легко отсчитывается его угловая высота.

Часто древним астрономам приходилось измерять не высоты светил, а углы между направлениями на два светила, например, на планету и какую-нибудь из звезд). Для этой цели весьма удобен был универсальный квадрант (рис. 5а). Этот инструмент был снабжен двумя трубками — диоптрами, из которых одна ( АС )неподвижно скреплялась с дугой квадранта, а вторая (ВС) вращалась вокруг его центра. Главная же особенность универсального квадранта — его штатив, с помощью которого квадрант можно было фиксировать в любом положении. При измерениях углового расстояния от звезды до планеты неподвижный диоптр направлялся на звезду, а подвижный — на планету. Отсчет по шкале квадранта давал искомый угол.