Малкольм Гладуэлл - Гении и аутсайдеры [Почему одним все, а другим ничего?]

Компьютерная программа, разработанная Шонфельдом, позволяет студентам учиться рассчитывать угловой коэффициент. Угловой коэффициент – как, я уверен, вы помните (или, точнее сказать, уверен, вы не помните, во всяком случае, я не помнил) – есть отношение противолежащего катета к прилежащему. Угловой коэффициент равен 1, поскольку интервал изменения абсциссы равен 5 и интервал изменения ординаты также равен 5.

Итак, Рене сидит за клавиатурой и пытается сообразить, какие числа нужно ввести, чтобы программа нарисовала абсолютно вертикальную линию, совпадающую с осью y. Те, кто еще помнит уроки математики, понимают, что это в принципе невозможно. У вертикальной линии «неопределенный» угловой коэффициент. Ее интервал изменения ординаты бесконечен: любое число на оси y, начиная с нуля и до бесконечности. А интервал изменения абсциссы на оси x равняется нулю. Бесконечность, поделенная на нуль, не является числом.

Но Рене и не догадывается, что она пытается решить задачу, у которой нет решения. По выражению Шонфельда, девушка пребывает в блаженном заблуждении. Профессору особенно нравится показывать эту запись, поскольку она наглядно демонстрирует, как Рене постепенно выходит из этого заблуждения.

Рене – медсестра. Она никогда прежде не интересовалась математикой и на работе ни имела с ней дела. Но случайно получив доступ к этой программе, уже не может от нее оторваться.

– Я хочу провести прямую линию, параллельную оси y, – начинает девушка. Шонфельд сидит рядом с ней. Рене взволнованно смотрит на него. – Я уже пять лет всем этим не занималась.

Она принимается экспериментировать, вводя различные числа.

– Если я изменю угловой коэффициент вот так… минус один… Мне нужно сделать эту линию прямой.

Линия на экране монитора меняется в зависимости от вводимых чисел.

– Ой, так не получается.

У Рене удивленный вид.

– Что ты хочешь сделать? – спрашивает ее Шонфельд.

– Я хочу провести линию, параллельную оси y. Что мне для этого нужно? Кажется, мне нужно что-то изменить вот здесь (она показывает на рамку, куда вводится число для оси y). Вот что я поняла: если ты ставишь вместо единицы двойку, то график резко меняется. Так, если мне нужно подняться выше, нужно менять дальше.

Это и есть «блаженное заблуждение» Рене. Она установила, что чем выше координата на оси y, тем больше поднимается линия. Из чего она делает вывод: вертикальную линию можно нарисовать, введя достаточно большую координату на этой оси.

– Думаю, двенадцати или тринадцати будет достаточно. А может быть, даже пятнадцати.

Она хмурится, пытаясь вместе с Шонфельдом разобраться, что к чему. Задает ему вопросы. Он осторожно подталкивает ее в нужном направлении. Она предпринимает одну попытку за другой, пробует один вариант за другим.

В какой-то момент она вводит 20. Линия немного поднимается.

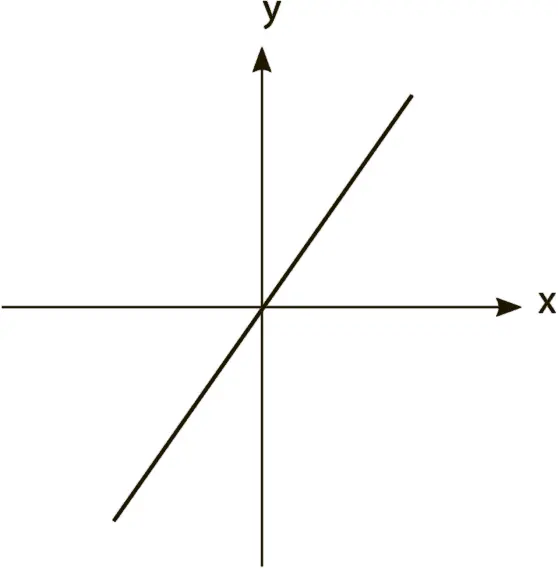
Она вводит 40. Линия поднимается еще выше.

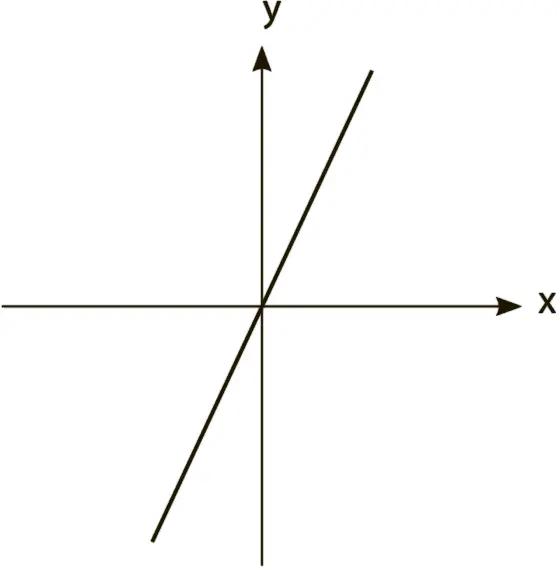
– Тут есть очевидное соотношение. Но никак не могу сообразить, что к чему… А если я введу восемьдесят? Если при сорока линия поднялась наполовину, тогда при восьмидесяти она должна подняться точно до оси y. Посмотрим, что у нас выйдет.

Она вводит 80. Линия поднимается еще выше, но все еще не вертикальна.

– А-а-а, это бесконечность, да? Линия никогда не будет совпадать с осью.

Рене близко подошла к решению. Но затем вновь возвращается к изначальному заблуждению:

– Так что же мне нужно сделать? Ввести сто? Каждый раз, когда число удваивается, линия приближается к оси наполовину. Но так и не доходит до нее. – Она вводит 100. – Уже ближе. Но все равно не совпадает.

Рене начинает думать вслух. Очевидно, ответ вот-вот будет найден.

– Ага, я так и знала… но… я знала. Больше число, выше линия. Только никак не могу понять, почему…

Она умолкает, глядя на экран монитора.

– Совсем запуталась. Одна десятая расстояния до единицы. Но я не хочу, чтобы…

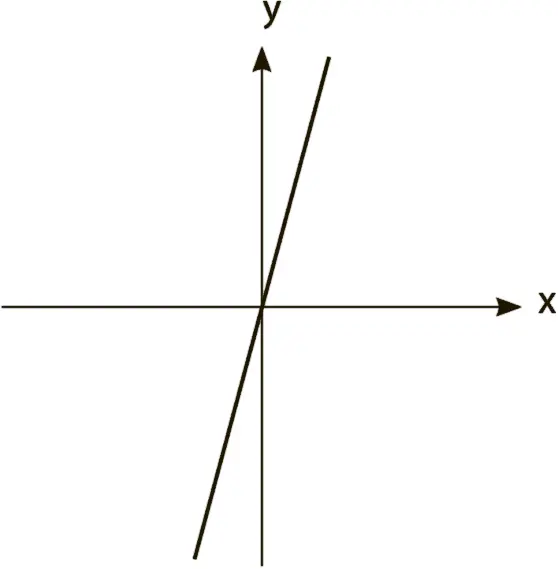
И тут ее осеняет.

– Ага! Любое число, поделенное на нуль! – Ее лицо светится от радости. – Вертикальная линия есть любое число, поделенное на нуль, а это неопределенное число. О-о-о! Ладно. Теперь все ясно. Угловой коэффициент вертикальной линии нельзя определить. А-а-а! Теперь в этом есть смысл. Никогда этого не забуду!

За годы своей работы Шонфельд записал на видео многих студентов, пытающихся решить те или иные математические задачи. Но запись с Рене – одна из его любимых, поскольку она идеально иллюстрирует то, что он считает ключом к изучению математики. От начала эксперимента до фразы «А-а-а, теперь в этом есть смысл» прошло двадцать две минуты . Это много. «Это задача для восьмого класса, – говорит Шонфельд. – Но если я посажу на место Рене обычного восьмиклассника, уверен, после нескольких попыток он скажет: “Я не понимаю”, “Объясните мне”».

Однажды Шонфельд спросил у учеников средней школы, как быстро они сдаются, решая какую-либо задачу, если она не выходит с первого раза. Ответы варьировались от тридцати секунд до пяти минут, средняя продолжительность попыток равнялась двум минутам.

Однако Рене не отступалась. Она экспериментировала, снова и снова перебирая разные варианты. Размышляла вслух. Не бросала дело на полпути. Не сдавалась.

На каком-то подсознательном уровне она чувствовала, что с ее «теорией» рисования вертикальной линии не все гладко, и не останавливалась до тех пор, пока не уверилась в своей правоте.

Рене не имела врожденных способностей к математике. Абстрактные понятия вроде «угловой коэффициент» и «неопределенный» давались ей с трудом. Именно поэтому Шонфельд считает ее пример наиболее впечатляющим.

«Ею движет желание разобраться, – говорит он. – Она не из тех, кто довольствуется поверхностным “да, вы правы” и успокаивается. И это очень необычно. – Он отматывает кассету назад и показывает на Рене, с искренним удивлением вглядывающуюся в экран монитора. – Смотрите, как она внимательно изучает график. Многие студенты ограничились бы беглым просмотром. Она же размышляет: “Это не согласуется с моими представлениями. Я не понимаю. Это важно. Я хочу вникнуть”. И когда она наконец находит объяснение, то говорит: “Да, теперь все сходится”».

В Беркли Шонфельд ведет курс по решению задач, в ходе которого он, по его собственному утверждению, старается отучить студентов от математических привычек, усвоенных в школе. «Я выбираю задачу, ответ на которую мне неизвестен, – поясняет он, – и предупреждаю студентов: через две недели вам предстоит показать решение. Ваши привычки мне хорошо знакомы.