Дуглас Кенрик - Инстинкты и смысл жизни. Почему в нас так много животного

Как показывает практика, так устроена вся общественная жизнь: мы сталкиваемся не с однонаправленной причинностью, а со сложными многонаправленными воздействиями. Мы стремимся оказать влияние на членов своей семьи, на соседей, коллег, а члены наших семей, соседи и коллеги в свою очередь пытаются оказать на нас ответное воздействие, они влияют друг на друга, что непосредственно сказывается по-разному на нас.

Поскольку вокруг постоянно происходит немало событий, люди влияют на окружающих, окружающие влияют на них, и в потоке многонаправленной обусловленности появляются новые произвольные векторы в виде случайных людей, то можно предположить, что реальность представляет собой рокочущий и жужжащий сумбур.

И тут мы подходим к важной мысли номер 2 — теоретики, изучающие системы, обнаружили, что природа — это самоорганизующаяся система. Порядок возникает как бы случайно и произвольно и поддерживается не надзирающей и управляющей силой, а простыми, эгоцентричными взаимодействиями между игроками внутри самой системы. Даже в самые неблагоприятные для нас с Лиамом дни мы умудряемся прибыть к дверям школы не позже сотен остальных семей, у каждой из которых свои внутренние конфликты и факторы влияния.

Любопытный вывод, полученный исследователями сложных систем, приводит нас к важной мысли номер 3 — ограниченное количество взаимодействующих переменных может вызвать огромные сложности. Как указывают Берт Холлдоблер и Эдвард Уилсон в своей книге «Сверхорганизм», у муравьев очень маленький мозг и небольшой набор простых инстинктивных правил, используемых при принятии решения, однако они способны создавать сложные колонии с легко приспосабливающимися организованными кастами, в которых существует разделение труда, где они решают разнообразные задачи и создают потрясающие жилища для своих колоний. Шон Кэрролл в своей книге «Самые прекрасные и бесконечные формы» говорит, что генетики были поражены, когда обнаружили, что генов оказалось гораздо меньше, чем они ожидали. Причем большое число этих генов является общим для совершенно различных видов, таких как тараканы и люди. Например, один и тот же ген отвечает за развитие шести лапок у насекомого и за развитие наших четырех конечностей. Но незначительные изменения, связанные с взаимодействием разных генов, имеют самые серьезные последствия.

Когда я тусовался с парнями в нагуталиненных ботинках, то умудрился завалить алгебру. Причина? Не выучил таблицу для запоминания тригонометрических функций. К моему сожалению, большинство из тех, кто занимается теорией комплексных систем, выражают свои мысли при помощи уравнений, а мой мозг реагирует на это так же, как на быструю итальянскую речь (тут же вспоминается сцена, когда мы стояли на железнодорожной платформе в Италии и пытались хоть что-то понять из объявления по громкоговорителю: «II treno per Firenze e appena partire al binario due; il treno di Milano e appena arrivare al binario cuatro; il treno di Venezia...» («Поезд во Флоренцию отправляется в... поезд из Милана прибывает в... поезд из Венеции...»)).

Но к моей радости, концепцию самоорганизации можно понять без всяких уравнений (и без итальянского), просто посмотрев на рисунки. Я был поражен, когда обнаружил, что самоорганизация предстает прямо перед глазами, если воспользоваться простой компьютерной программой составления таблиц. Как-то вечером, наслушавшись, как Гай Ван Орден и моя коллега Сэнди Брэйвер обсуждают исследование Латанэ о распространении влияний в группах, я пришел домой и нарисовал на экране простую матрицу, состоящую из черных, белых и серых элементов, такую, как на рис. 12.1.

Представьте себе такую картину: соседям нужно проголосовать по поводу введения специального налога на строительство новой школы. Давайте предположим, что поначалу мы имеем разброс мнений, то есть они распределены произвольно по отношению друг к другу. Предположим также, что потом ваши соседи начинают обсуждать вопрос с соседями, живущими поблизости, и приходят к мысли, что не будут поддерживать позицию, не пользующуюся популярностью. После того как я изобразил это схематически, подобно тому, как это сделано на рис. 12.1, я задал такие параметры в программе Excel, которая автоматически обновляла решение каждого соседа с учетом общего изначального мнения близких соседей.

После первого этапа обсуждения сосед из третьего дома внизу слева изменил свою позицию с отрицательного ответа на положительный, а кое-кто из его соседей, наоборот, изменил «да» на «нет». Окончательная раскладка всегда отличалась от начальной и зависела от того, на какой случайной схеме я первый раз включил свой компьютер. Тем не менее всего после нескольких обновлений крапчатая структура исчезала, вся схема как-то упрощалась и приобретала более однородный вид. В этом случае, если каждый сосед в конце концов принимал решение согласиться с большинством, все соседи оказывались объединенными в оппозицию и схема выглядела таким образом, как в квадрате Сценарий 1.

Системы, подобные этой, вначале очень нестабильны, и даже самые незначительные различия на начальном этапе могут оказать огромное влияние на вид окончательного соотношения. Например, в Сценарии 2 (правый верхний квадрат) изображено, что произойдет, если всего лишь один человек (отмечен серым) не согласится с большинством, а будет настроен скорее голосовать «за». Этот человек, к примеру Альберта, изменила бы «да» на «нет», только если бы ее соседи были единогласно против; но если хоть один был бы готов голосовать «за», Альберта тоже не изменила бы свое решение и проголосовала «за». Этот отдельно взятый одиночка с собственным мнением в этом случае оказывает такое большое влияние, что постепенно все соседи делятся на два лагеря (Сценарий 2) — южный лагерь, готовый голосовать «за», и северный — «против». На нижнем правом квадрате (Сценарий 3) видно, что произойдет, если в северном лагере появится одиночка, назовем ее Агнесс (тоже отмечена серым), с положительным мнением. Эти двое смогли бы полностью изменить единодушное решение соседей.

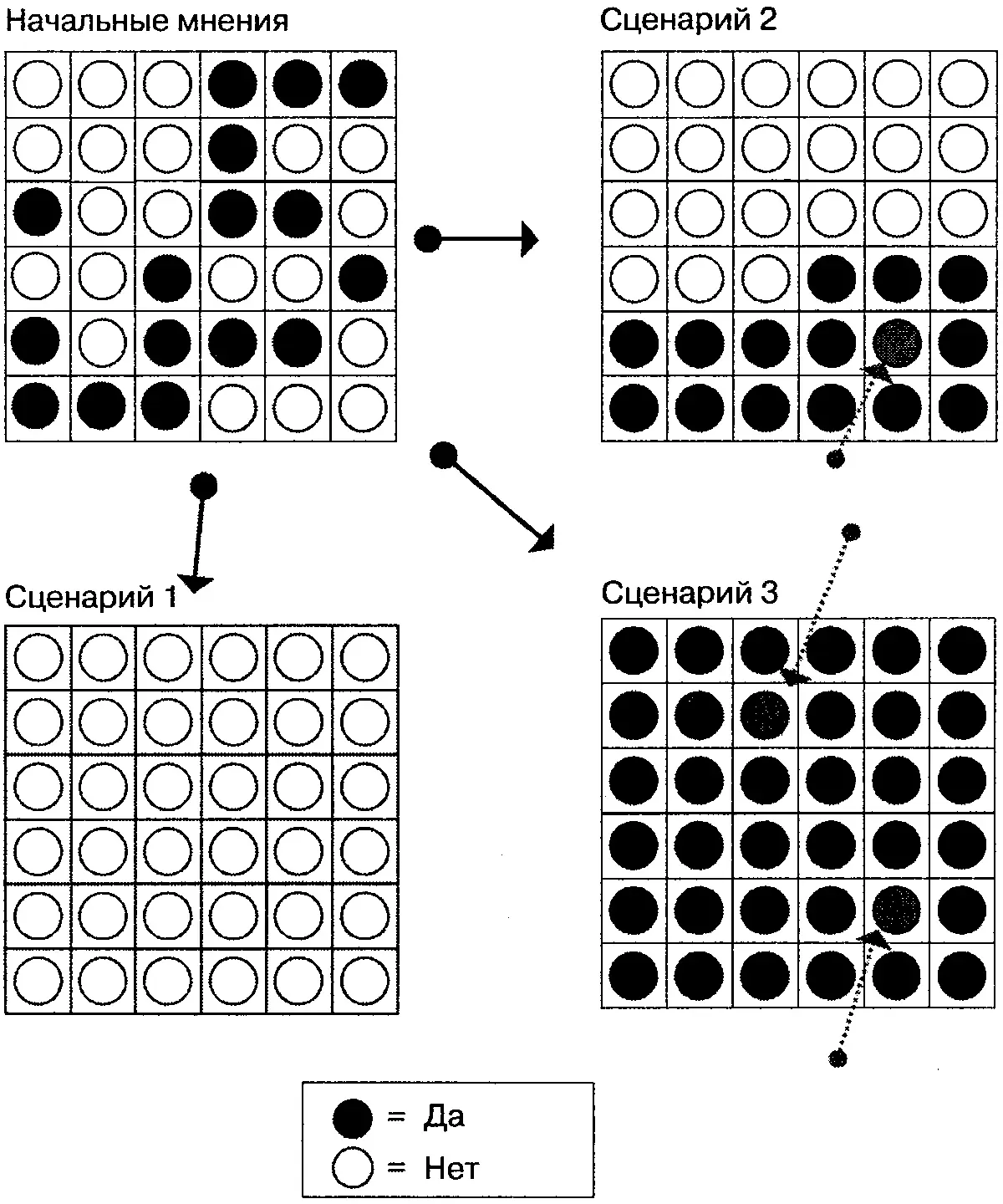
Рис. 12.1.Самоорганизация соседей. Верхний левый квадрат — это соседи, у которых разделились мнения по какому-то вопросу. Учитывая, что каждый из них хочет примкнуть к большинству, то через несколько раундов переговоров непосредственные соседи все по очереди присоединятся к оппозиции. Если один или двое соседей твердо придерживаются более подходящей, с их точки зрения, позиции (это серые одиночки справа), то окончательная картина может выглядеть совершенно иначе (как описано в тексте)