Анна Анастази - Дифференциальная психология. Индивидуальные и групповые различия в поведении

Подобно другим методам статистики, частотное распределение представляет собой суммирование и обработку количественных данных, которые производятся для понимания общей картины и выявления существенных тенденций. Результаты тестирования или любые другие серии измерений группируются в классы, и все случаи, лежащие внутри каждого класса, заносятся в таблицу. Таблица 1 представляет собой пример такого частотного распределения. В ней приводятся результаты тестирования 1000 студентов колледжа на умение применять код, в котором необходимо было один набор бессмысленных слогов заменить на другой. Данные, показывающие количество правильно замененных за две минуты слогов, находились в интервале от 8 до 52. Они были сгруппированы по интервалам (по 4 пункта в каждом), начиная с 52–55 на верхней точке распределения и заканчивая 8—11 на нижней. Колонка под названием «частота» в таблице 1 показывает количество людей, чьи результаты лежат в этих интервалах. Например, показатели, находящиеся в пределах 52 и 55, зафиксированы только у одного человека, значения между 48 и 51 — тоже у одного, а значения между 44 и 47 — у двадцати и так далее. Очевидно, что результаты данного теста гораздо легче увидеть при помощи такого распределения, чем рассматривая лист, содержащий 1000 первичных результатов.

Еще удобнее иметь дело с показателями частотного распределения, если изобразить их графически. Рисунок 2 представляет данные таблицы 1 в графической форме. На горизонтальной оси даны результаты, сгруппированные в интервалы; числа на вертикальной оси означают количество случаев внутри каждого интервала.

График сделан в двух формах, которые обычно широко используются. Одна графическая форма называется полигоном частот, в котором число индивидов внутри каждого интервала обозначено точкой, расположенной напротив центра интервала; последовательность точек затем была соединена прямыми линиями. Другая графическая форма образуется прямыми колонками, или прямоугольниками, основаниями которых служат интервалы высота каждой колонки зависит от числа случаев в данном интервале. Такая графическая форма называется гистограммой. Если взглянуть, например, на интервал 44–47 в таблице 1, то можно найти 20 случаев результирующих значений, находящихся в его пределах. Соответственно на рисунке 2 точка ставится на пересечении проекции от 20 и проекции центра интервала 44–47. Мы получаем одну из точек, необходимых для построения частотного полигона. В гистограмме те же 20 случаев представлены колонкой 44–47 интервала, ограниченной сверху проекцией числа 20, находящегося на вертикальной оси.

Таблица 1 Частотное распределение данных 1000 студентов колледжа, тестирование умения применять код. (Данные из Анастази, 2, с. 34.)

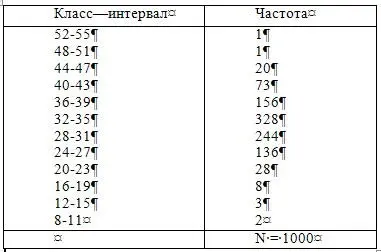
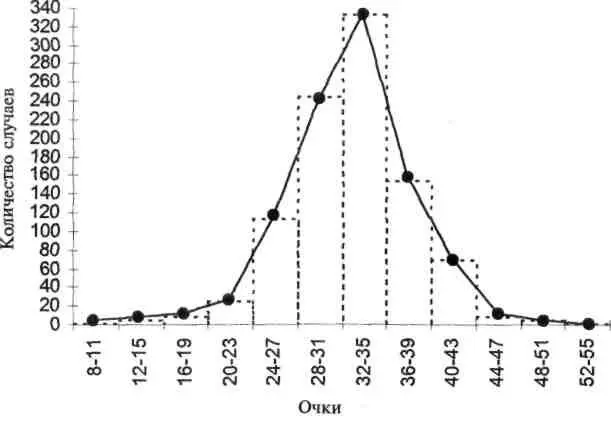
Рис. 2. График распределения: полигон частот и гистограмма. (Данные из таблицы 1.)

Мы можем продолжить описание группы, определив ее центральную тенденцию. Если мы захотим получить наиболее типичное значение, которое характеризовало бы группу в целом, то необходимо определение главной тенденции. Одним из наиболее известных способов является вычисление средней величины, получаемой при сложении всех показателей и делении полученной суммы на число случаев. Такая величина называется средним арифметическим.

Другим способом определения главной тенденции, часто используемым в психологии, является медианный. Если все результирующие значения расположить по порядку в соответствии со своей величиной, то медианой будет результат, расположенный ровно посередине ряда. Для больших групп гораздо легче вычислить медиану непосредственно на основе частотного распределения. В этом случае медианная точка разделяет распределяемое множество таким образом, что половина случаев будет находиться выше нее, а другая половина — ниже. Еще одним способом измерения главной тенденции, иногда встречающимся в психологических исследованиях, является определение моды, или наиболее часто встречающегося показателя. Его так же можно найти на основе частотного распределения, выявив ту точку интервала, которая имеет самую большую частоту. Заметим, что мода соответствует самой высокой точке графика. Для распределения, данного в таблице 1 и на рисунке 2, среднеарифметическое значение составляет 32,37, медианное — 32,46 и значение моды — 33,5.

Читатель наверняка уже обратил внимание на особенности распределения, представленного в таблице 1 и на рисунке 2. Большинство случаев расположены в центре ряда, а приближаясь к крайним значениям, происходит долгий плавный спад. На графике нет разрывов — нет классов, которые были бы отделены друг от друга. Кроме этого, график по обе стороны симметричен; это означает, что если его разделить вертикальной линией по центру, то получившиеся две половинки окажутся примерно одинаковыми. Такой график распределения своей формой похож на колокол, это так называемое «нормальное распределение», которое чаще всего встречается при измерениях индивидуальных различий. В своем идеальном виде нормальное распределение изображено на рисунке 3.

Понятие нормального распределения в статистике используется уже давно. Вероятность какого-либо события представляет собой частоту его наступления, зафиксированного очень большим количеством наблюдений. Эта вероятность представляет собой определенное соотношение, точнее, дробь, числителем которой является ожидаемый результат, а знаменателем — все возможные результаты. Таким образом, вероятность, или шансы, того, что две монеты выпадут одной и той же стороной, например решкой, будет один к четырем, или 1/ 4. Это следует из того факта, что существует всего четыре возможные комбинации выпадения монет РР, РО, ОР, ОО, где Р — решка, а О — орел. Одна из четырех, РР, означает выпадение только решек. Вероятность выпадения двух орлов будет также составлять 1/ 4, а вероятность выпадения решки какой-либо одной монеты при выпадении орла другой составит один к двум, или 1/ 2. Даже если число монет увеличить, скажем, до 100, и количество возможных комбинаций станет очень большим, то мы по-прежнему сможем математически определить вероятность возникновения каждой комбинации, например, выпадения всех решек или 20 решек и 80 орлов. Эти вероятности, или ожидаемую частоту выпадений, можно изобразить графически описанным выше методом. Если число монет будет очень велико, то построенный график окажется колокольной формы, то есть графиком нормального распределения.