Дмитрий Узнадзе - Психология установки

В поставленных для разрешения этого вопроса опытах [19] А. Авалишвили. К вопросу об установочной роли критических экспозиций в опытах на установку // Психология 1942. Т. 1. испытуемые получали в критической серии, после пятикрат­ного засвидетельствования равенства предлагаемых объек­тов, чуть отличающиеся друг от друга по величине фигуры, а именно круги в 20-21 мм, 20-22 мм, 20-23 мм и 20-24 мм в диаметре, а также квадраты — в 15-16 мм, 15-17 мм, 15- 18 мм и 15-19 мм. Точнее, эксперименты протекали в следу­ющем порядке: испытуемые получали в установочных опы­тах пару контурных кругов (20-36 мм) 15 раз. Затем следо­вали критические опыты: пара равных контурных кругов (20-20 мм). После пятикратного констатирования их равен­ства испытуемым подменивали эти равные критические кру­ги неравными (20-21 мм). Если круги продолжали казаться равными, они снова подменивались сначала кругами в 20- 22 мм, затем — в 20-23 мм и, наконец, — в 20-24 мм.

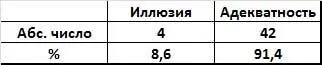
Какие же результаты были получены в этих опытах? При экспозиции пары критических кругов в 20-21 мм были по­лучены результаты, суммированные в табл. 12. Мы видим, что в данном случае иллюзии возникли из 46 только у 4 ис­пытуемых, а остальные 42 дали вполне адекватные ответы.

В следующей серии опытов испытуемым были предложе­ны круги, отличающиеся друг от друга в диаметре на 2 мм. Здесь получились еще более показательные результаты: ока­залось, что в этом случае все 11 лиц, которые были допуще­ны к опытам (в этой серии принимали участие лишь те лица, которые в предыдущих опытах уже с самого начала или по­сле лишь некоторого колебания дали пятикратную иллю­зию), констатировали факт неравенства критических кругов.

Таблица 12.

Чтобы не осталось сомнения, что, быть может, здесь игра­ет роль фактор фигуры, познакомимся с результатами опы­тов с другой фигурой, с квадратами. Здесь при опытах с различиемв 1 мм (15-16 мм) результаты оказались точь-в-точь те же, что и при кругах с той же разницей в диаметре. Три че­ловека имели иллюзию, а 43 оценивали соотношение фигур совершенно правильно. Что же касается квадратов, отлича­ющихся друг от друга на 2 мм (15-17 мм), то полученные в этомслучае данные свидетельствуют, что случаи иллюзии встречаются лишь в виде исключения (3 человека из 43, тог­да как правильная оценка здесь в порядке вещей).

Мы не приводим данных, полученных в других сериях аналогичных опытов (заполненные круги вместо контурных в первой серии, контурные квадраты вместо заполненных в предыдущей серии); в сущности, они повторяют выводы предшествующих опытов, ничего существенного к ним не прибавляя.

Таким образом, мы можем утверждать, что многократ­ное повторение показаний равенства фактически неравных объектов в критических опытах далеко не означает факта фиксации этого равенства.

Но это заключение можно было бы признать достоверным лишь в том случае, если бы мы были уверены, что критиче­ские объекты воспринимаются адекватно, т. е. как неравные, именно в связи с отсутствием установки, фиксированной на равенство, а не потому, что неравенство критических объек­тов слишком явно и, таким образом, не может быть ассими­лировано установкой, фиксированной на равенство.

Нам необходимо проверить это предположение. Допус­тим, что у нас имеется установка, фиксированная специаль­но на равенство, и предложим испытуемому с такой установ­кой в качестве критических объектов интересующие нас в этом случае фигуры (круги, отличающиеся друг от друга в радиусе на 1-2 мм). Если установка на самом деле окажется бессильной ассимилировать это различие, то мы получим от испытуемого правильные показания относительно неравен­ства предложенных ему фигур; если же нет, тогда фигуры эти будут казаться равными.

Проверить это не представляет трудности. Но этого и не нужно, У нас есть опыты, из которых можно почерпнуть от­вет на поставленный здесь нами вопрос [20] Р. Г. Натадзе. К вопросу о выработке установки на равенство // Труды Тбилис. гос. ун-та. 1941. Т. XVII. .

В этих опытах у испытуемых фиксировалась установка на равенство геометрических фигур (кругов и квадратов), а за­тем им экспонировались в качестве критических фигуры, от­личающиеся друг от друга по величине на 1,5 мм и 1 мм (кру­ги диаметром 22,5-24 мм и квадраты с длиною сторон 21- 22 мм). Результаты оказались вполне соответствующими указанным нами предположениям, а именно; общее число лиц, дающих иллюзию хотя бы на одну из критических фи­гур под влиянием установочных опытов, доходит до 30, т. е. до 70,1% общего числа (42) испытуемых.

Следовательно, не может быть сомнения, что при наличии соответствующей установки различие фигур на 1-2 мм не играет роли: оно не мешает проявиться ассимилирующему влиянию фиксированной установки.

Это значит, что раз в описанных выше опытах различие фигур на 1-2 мм никогда не оставалось незамеченным, т. е. эти различия там никогда не ассимилировались, соответству­ющей фиксированной установки там вовсе и не было.

Таким образом, хможно считать установленным, что в на­ших обычных опытах повторная апперцепция равных кругов как равных вовсе не играет роли установочных экспозиций и не фиксирует совершенно никакой новой, соответствую­щей им, установки. Пока равные фигуры воспринимаются как неравные, продолжает действовать все та же фиксиро­ванная в установочных опытах установка. Когда же испыту­емый начинает повторно воспринимать их как равные, то в основе этого лежит уже не фиксированная на равенство, а адекватная настоящему положению вещей установка.

Итак, нет сомнения, что критические экспозиции не фик­сируют никакой новой установки. Они содействуют лишь проявлению установки, адекватной данной ситуации.

2. Временное затухание установки.Как было указано выше, спустя некоторое время после прекращения критиче­ских опытов повторное предложение этих последних снова начинает вызывать те же обычные установочные иллюзии.

Спрашивается, как понять это?

Не подлежит сомнению, что в результате воздействия критических эксиозиций фиксированная ранее установка не окончательно ликвидируется: по всей видимости, она отсту­пает перед непрерывным рядом воздействий критических экспозиций, совершенно не соответствующих ей, уступая ме­сто адекватной им установке. В тех случаях, в которых выра­ботанная в фиксированных опытах установка достаточно прочна, это происходит лишь временно, под влиянием посто­янного, непрерывного воздействия критических экспозиций. Следовательно, стоит пройти этому периоду непрерывного действия критических экспозиций, чтобы сила фиксации снова дала себя почувствовать, снова вернула бы себе способ­ность вызывать к жизни соответствующие ей обычные иллю­зии установки.