Эрл Гейтс - Введение в электронику

RТ = 357.27 Ом

ПРИМЕР: Каково должно быть сопротивление резистора, подключенного параллельно резистору в 47 Ом для того, чтобы общее сопротивление цепи было 27 Ом? См. рис. 4-22.

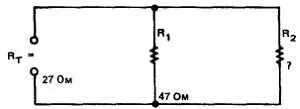
Рис. 4-22

Дано:

RТ = 27 Ом; R1 = 47 Ом;

R2 =?

Решение:

1/ RТ = 1/ R1 + 1/ R2

1/27 = 1/47 + 1/ R2

0,0370 — 0,0213 = 1/ R2

R2 = 63,69 Ом

Заметим, что 63,69 ома не является стандартным номиналом резистора. Используйте резистор с ближайшим стандартным номиналом, который равен 62 ома.

4–5. Вопросы

1. Напишите формулу для определения общего сопротивления параллельной цепи.

2. Каково общее сопротивление цепи, содержащей три резистора — 1500 Ом, 3300 Ом и 4700 Ом — соединенных параллельно? (Сначала нарисуйте цепь).

Последовательно-параллельная цепь является комбинацией последовательной и параллельной цепей. На рис. 4-23 показана простая последовательно-параллельная цепь, состоящая из резисторов. Заметим, что R 2и R 3соединены параллельно и эта параллельная комбинация соединена последовательно с R 1и R 4. Ток течет от отрицательного вывода источника тока через резистор R 4и делится в точке А , протекая через две ветви R 2и R 3. В точке В ток соединяется и протекает через R 1.

Общее сопротивление последовательно-параллельной цепи вычисляется с помощью формул для последовательного соединения:

R T= R 1+ R 2+ R 3+…+ R n,

и параллельного соединения:

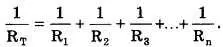
Большинство цепей может быть разбито на простые параллельные и последовательные цепи. Процедура вычисления общего сопротивления состоит из следующих этапов:

1. Вычисление общего сопротивления параллельных участков цепи для определения эквивалентных сопротивлений.

2. Если в параллельных участках цепи есть последовательно включенные сопротивления, то сначала нужно вычислить эквивалентное сопротивление последовательно включенных элементов цепи.

3. После вычисления эквивалентных сопротивлений перерисуйте цепь, заменяя параллельные участки цепи эквивалентными сопротивлениями.

4. Проведение окончательных вычислений.

ПРИМЕР: Чему равно полное сопротивление цепи, показанной на рис. 4-23?

Первый шаг — это определение эквивалентного сопротивления ( RА) участка, содержащего R2 и R3.

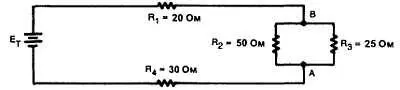
Рис. 4-23

Дано:

R2 = 50 Ом; R3 = 25 Ом

RА =?;

Решение:

1/ RА = 1/ R2 + 1/ R3

1/ RА = 1/50 + 1/25 = 3/50

1/ RА = 1/50 + 2/50 = 3/50

RА = 50/3

RА = 16,7 Ом

Перерисуем цепь, подставив эквивалентное сопротивление параллельного участка. См. рис. 4-24.

Рис. 4-24

Теперь определим полное сопротивление последовательной эквивалентной цепи.

Дано:

R1 = 20 Ом; Ra = 16,7 Ом; R4 = 30 Ом

RТ =?

Решение:

RТ = R1 + Ra + R4

RТ = 20 + 16,7 + 30

RТ = 66,7 Ом

ПРИМЕР: Вычислить полное сопротивление цепи, изображенной на рис. 4-25.

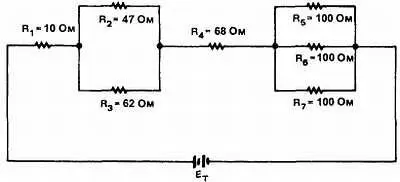
Рис. 4-25

Сначала найдем эквивалентное сопротивление ( RA) параллельно соединенных резисторов R2 и R3. После этого найдем эквивалентное сопротивление ( RB) параллельно соединенных резисторов R5, R6 и R7.

Дано:

R2 =47 Ом; R3 =62 Ом

RA =?

Решение:

1/ RА = 1/ R2 + 1/ R3

1/ RА = 1/47 + 1/62

1/ RА = 0,0213 + 0,0161 = 0,0374

RА = 1/0,0374 = 26,7 Ом

* * *

Дано:

R5 = 100 Ом, R6 = 100 Ом; R7 = 100 Ом

RB =?

Решение:

1/ RВ = 1/ R5 + 1/ R6 + 1/ R7

1/ RВ = 1/100 + 1/100 + 1/100 = 3/100

RВ = 100/3 = 33,3

Теперь перерисуем цепь, используя эквивалентные сопротивления RA и RB и определим полное сопротивление эквивалентной последовательной цепи. См. рис. 4-26.

Рис. 4-26

Дано:

R1 = 10 Ом; RА = 26,7 Ом; R4 = 68 Ом; RB = 33,3 Ом.

RT =?

Решение:

RT = R1 + RА + R4 + RB

RT = 10 + 26,7 + 68 + 33,3

RT = 138 Ом.

Цепь, показанная на рис. 4-25, может быть заменена одним резистором номиналом 138 Ом (рис. 4-27).

Рис. 4-27

ПРИМЕР: Найдите полное сопротивление цепи, изображенной на рис. 4-28.

Рис. 4-28

Эквивалентное сопротивление последовательного участка в параллельной цепи должно определяться первым. Оно обозначено Rs.

Дано:

R2 = 180 Ом; R3 = 200 Ом; R4 = 620 Ом

Rs =?

Решение:

Rs = R2 + R3 + R4

Rs = 180 + 200 + 620

Rs = 1000 Ом.

Перечертим цепь, заменяя последовательно соединенные резисторы R2, R3 и R4 эквивалентным сопротивлением Rs. См. рис. 4-29.

Рис. 4-29

Определим эквивалентное сопротивление RA параллельно соединенных резисторов Rs и R5

Дано:

Rs = 1000 Ом; R5 = 1000 Ом.

RA =?

Решение:

1/ RA = 1/ Rs + 1/ R5

1/ RA = 1/1000 + 1/1000 = 2/1000

RA = 500 Ом

Перерисуем цепь опять, заменив параллельно соединенные резисторы Rs и R5 эквивалентным сопротивлением RA, и определим полное сопротивление полученной последовательной цепи. См. рис. 4-30.

Дано:

R1 = 2700 Ом; RA = 500 Ом; R6 = 5600 Ом.

RT =?

Решение:

RT = R1 + RA + R6

RT = 2700 + 500 + 5600

RT = 8800 Ом.

Рис. 4-30

Цепь, показанная на рис. 4-28, может быть заменена одним резистором сопротивлением 8800 Ом (рис. 4-31).

Рис. 4-31

4–6. Вопрос

1. Чему равно полное сопротивление цепи, в которой резисторы 1500 Ом и 3300 Ом соединены параллельно, а затем последовательно с резистором 4700 Ом? (Сначала нарисуйте цепь).