Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

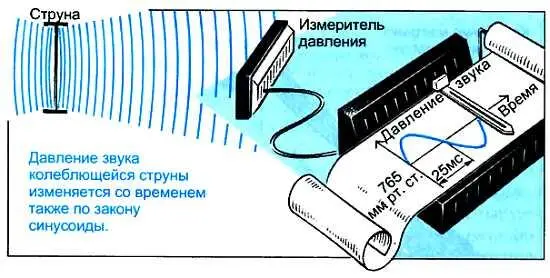
Правда, струна колеблется намного быстрее: в секунду она совершит не одно-два, а десятки и сотни колебаний. Например, самая толстая (басовая) струна рояля, "обладающая" самым низким звуком, колеблется при ударе на клавишу с частотой 27 Гц. Струны гитары издают более высокие звуки, они совершают колебания с частотами от 144 Гц (самая толстая струна) до 576 Гц (самая тонкая струна). Наиболее высокую частоту колебаний звука в оркестре (9000 Гц) имеет флейта-пикколо.

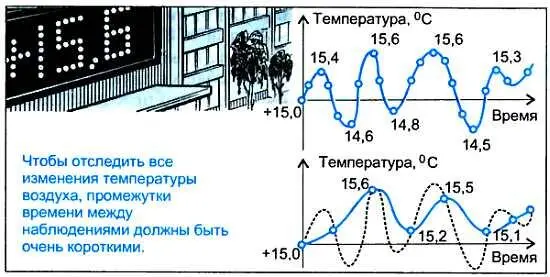
Вам приходилось когда-нибудь в погожий весенний день наблюдать за показаниями температуры на городском световом табло? Уже ласково светит солнце, хотя в воздухе еще прохладно. Вот краешек солнца закрыла тучка, и температура чуть понизилась. Тучка прошла — и вновь стало теплее. Дуновение ветра также заставляет "скакать" цифры на электронном табло. Если через очень короткие промежутки времени (скажем, через 1 с) наносить значения температуры воздуха на график, то получим множество точек, отражающих изменения температуры. Таким образом, имеем дело не с непрерывной кривой изменения температуры, а лишь с ее значениями, отсчитанными через определенные промежутки времени. По сути говоря, мы описали некоторый непрерывный процесс последовательностью десятичных цифр.

От десятичной системы счисления легко перейти к двоичной системе счисления (см. главу "Внимание: конкурент!"). И пусть нас не смущает, что температура выражается не целым числом. Можно просто-напросто не обращать внимания на запятую, отделяющую десятые доли градуса, и записывать в двоичной форме, например, не число 15,6 °C, а число 156: ведь знаем же мы, в конце концов, что температура воздуха не может выражаться ни числом 1,56 (так как она высвечивается на табло с точностью до десятых долей градуса), ни числом 156.

Невыясненным остался вопрос, как часто следует брать отсчетные значения непрерывной кривой, чтобы отследить все ее изменения. Так, при более длительных промежутках времени между наблюдениями за температурой воздуха не удастся отследить все ее быстрые изменения.

Давление звуковой волны, распространяющейся от струны, изменяется во времени по закону синусоиды. Чтобы отследить все ее изменения, очевидно, достаточно брать отсчетные значения в моменты, соответствующие максимумам и минимумам синусоиды, т. е. с частотой, превышающей, по крайней мере, вдвое частоту звукового колебания. Например, если струна совершает 20 колебаний в секунду (частота 20 Гц), максимальное звуковое давление будет наблюдаться через каждую 1/20 с, т. е. через 50 мс. (Напомним, что 1 с = 1 000 мс = 1 000000 мкс = 1 000000000 нс.) Максимумы и минимумы кривой звукового давления разделены интервалами в 25 мс.

Значит, отсчетные значения но кривой должны следовать не реже, чем через 25 мс, или с частотой 40 отсчетов в секунду (40 Гц). Обычно отсчетные значения на кривой берут "с запасом": не в 2 раза чаще, чем колеблется звук, а, скажем, в 10 раз. В этом случае они очень хорошо передают форму кривой.

Интересен случай, когда звуковые волны излучаются двумя одновременно колеблющимися струнами. На рисунке показаны три варианта: вторая струна колеблется в 2, 3 и 10 раз чаще, чем первая. Давления двух звуковых волн на пластину, помещенную на их пути, складываются. График результирующего давления уже не является синусоидой. Мы видим, что быстрые изменения этой кривой обусловлены более высокочастотным колебанием (в данном случае колебанием второй струны). Поэтому для того чтобы отследить все быстрые изменения результирующего звукового давления, отсчетные значения следует брать с частотой, по крайней мере, вдвое превышающей частоту колебания второй струны. В последнем варианте частота взятия отсчетных значений должна превышать 400 Гц. Это означает, что отсчетные значения должны следовать не реже чем через 1/400 = 0,0025 с = 2,5 мс, а лучше — еще чаще, например через 0,5 мс.

До сих пор мы намеренно упрощали задачу, когда считали, что давление звуковой волны, создаваемой струной, изменяется по закону синусоиды. На самом деле это не так. График колебания реальной струны, а следовательно, график звукового давления, отличается от синусоиды. Дело в том, что всякое вибрирующее тело создает одновременно звуки нескольких частот или, как говорят, тонов. Самый низкий из них называют основным тоном, более высокие тоны, сопровождающие основной, — обертонами. При звучании гитары, скрипки, рояля всегда слышны кроме основного тона дополнительные призвуки, т. е. обертоны. Так, если принять частоту основного тона (синусоидальное колебание) равной 20 Гц, то частоты обертонов (тоже синусоидальные колебания) составят: первого — 40 Гц; второго — 60 Гц, третьего — 80 Гц и т. д., а, скажем, десятого обертона — 200 Гц. В совместном звучании основной тон и обертоны создают соответствующую окраску звука, или тембр. Один тембр отличается от другого числом и силой обертонов.

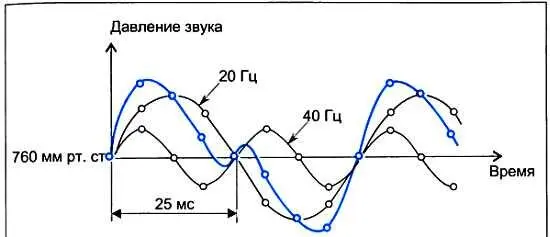
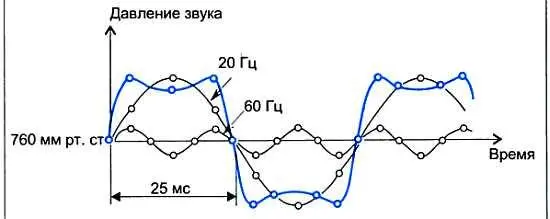
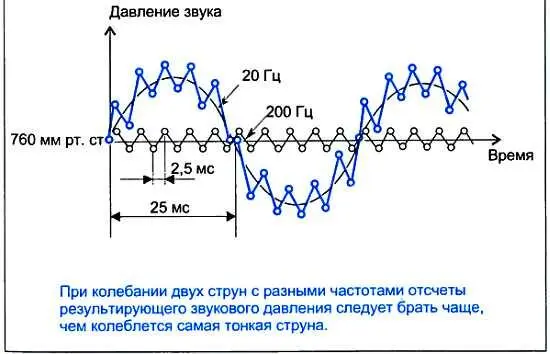
Таким образом, для получения формы кривой звукового давления, создаваемого колеблющейся струной гитары или скрипки, нужно сложить синусоидальные кривые звуковых давлений основного тона и обертонов. Подобная операция была проделана, когда рассматривали одновременные колебания двух струн. Только в данном случае из-за наличия большого числа обертонов форма результирующей кривой будет еще сложнее, т. е. еще сильнее отличаться от синусоидальной. Совершенно ясно, что для отслеживания самых быстрых изменений звукового давления отсчетные значения на результирующей кривой придется брать с частотой в несколько раз выше (по крайней мере, в 2 раза) частоты последнего обертона.

Графики давления звуковых волн, создаваемых человеческим голосом, имеют еще более сложную форму.

Человек набрал в легкие воздух и издал звук. Что же произошло? Воздух, выходя из легких, заставляет вибрировать голосовые связки. От них колебание воздуха передается через гортань голосовому аппарату, заканчивающемуся ротовой и носовой полостями. Последние выполняют роль резонаторов — они усиливают колебания воздуха, подобно тому как полый корпус гитары или скрипки, также являясь резонатором, усиливает звуки струн. Колебания воздуха из голосового аппарата человека передаются окружающему воздуху. Возникает звуковая волна. Характер издаваемого звука определяется натяжением голосовых связок, формой ротовой полости, положением языка, губ и т. д.