Рудольф Сворень - Шаг за шагом. Транзисторы

В качестве примера такой зависимости рассмотрим, разумеется упрощенно, как возникает ток в цепи слюдяного конденсатора под действием переменного напряжения.

Как известно, свободные заряды через диэлектрик, в данном случае через слюду, конденсатора пройти не могут. Но под действием приложенного напряжения несколько сдвигаются, деформируются электронные орбиты атомов слюды. Происходит некоторое небольшое движение электронов (оно называется током смещения), но без их выхода из атомов. В результате деформации орбит с одной стороны диэлектрика (именно с той стороны, куда сместились орбиты) появляется отрицательный заряд, а с другой стороны появляется положительный заряд. Эти заряды притягивают или отталкивают свободные электроны в проводниках, подключенных к конденсатору, и в этих проводниках возникает ток проводимости. Однако все эти события — смещение орбит и движение электронов в проводниках — происходят лишь в тот момент, когда меняется напряжение, подведенное к конденсатору.

Если к конденсатору приложено постоянное напряжение, пусть даже очень большое, то смещенные некогда орбиты находятся в состоянии покоя и никакого движения зарядов, никакого тока в конденсаторе и во внешней цепи нет. Но стоит только напряжению измениться, как заряды совершат некоторый дополнительный сдвиг: при увеличении напряжения — в одну сторону, при уменьшении — в другую. Отсюда вывод: ток в цепи конденсатора протекает только в момент изменения напряжения. И еще один вывод: чем быстрее меняется напряжение, тем быстрее смещаются заряды, тем больше ток в цепи. Вот почему график тока через конденсатор по сути дела представляет собой график скорости изменения напряжения, приложенного к этому конденсатору. Графики эти всегда различны по форме (рис. 25), за исключением только одного случая — синусоидального напряжения. Только синусоидальное напряжение создает в цепи конденсатора ток такой же формы — синусоидальный переменный ток. Это замечательное и уникальное свойство синусоидального сигнала проявляется не только в конденсаторах, но еще и в катушках и трансформаторах, во всех так называемых реактивных элементах электрических цепей.

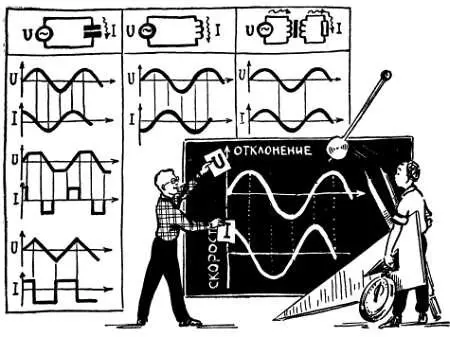
Рис. 25. Ток в цепи конденсатора протекает только при изменении напряжения на нем, и поэтому графики напряжения и тока (кроме синусоиды) различны.

Наконец, третье «за». Выбрав квадрат в качестве стандартной составляющей при разметке поверхности моря на карте, мы можем довольно просто расчертить эту поверхность, а если нужно, даже разрезать ее на составляющие. Вырезать квадрат из бумаги не составляет никакого труда. Подобно этому любой сложный сигнал можно довольно просто разделить на синусоидальные (именно на синусоидальные!) составляющие. Делается это с помощью резонансных электрических фильтров, в частности с помощью колебательных контуров. Такой контур состоит из соединенных друг с другом конденсатора и катушки (Воспоминания № 18 и № 20).

Если ввести в контур порцию электрической энергии, зарядив конденсатор или создав магнитное поле в катушке, то в контуре начнутся свободные колебания, появится переменный ток. Этот процесс очень напоминает колебания гитарной струны, которой вы также передаете порцию энергии, тронув эту струну пальцами. И, подобно тому как частота колебаний струны зависит от ее массы и силы натяжения (чем тоньше струна и чем сильнее она натянута, тем выше частота колебаний), подобно этому частота электрических колебаний в контуре зависит от емкости С конденсатора и индуктивности L катушки. Чем меньше емкость С и индуктивность L , тем выше частота колебаний.

Переменный ток, который возникает в колебательном контуре, по форме очень близок к синусоиде (в идеальном контуре, без потерь энергии, график тока — это настоящая, идеальная синусоида). Определенным образом включив колебательный контур в цепь со сложным сигналом, мы увидим, что контур выделит из этого сигнала синусоидальную составляющую своей собственной частоты (если, конечно, такая составляющая есть в сигнале). Пропустив сложный сигнал через достаточное количество настроенных контуров, можно выделить из этого сложного сигнала все его синусоидальные составляющие.

Можно не сомневаться, что после трех высказанных «за» простейшие синусоидальные сигналы будут без возражений утверждены в должности стандартных составляющих сложного сигнала. Синусоидальные колебания часто называют гармоническими, а синусоидальные составляющие сложного сигнала — гармониками. Любой сложный сигнал принято официально характеризовать его спектром — набором гармоник с указанием их амплитуды. А результат прохождения сигнала по какой-либо цепи можно оценивать по тому, как изменился его спектр, какие новые гармоники появились в этом сигнале, какие усилились, какие ослабились. Именно с этих позиций мы и рассмотрим сейчас работу полупроводникового диода.

Включим диод в схему простейшего выпрямителя (рис. 26) и подведем к нему синусоидальное переменное напряжение.

Рис. 26. Под действием переменного напряжения в цепи диода протекает пульсирующий ток, который состоит из постоянной и переменной составляющих.

Для простоты будем считать, что диод имеет идеальную характеристику, что его обратный ток равен нулю, то есть обратное сопротивление бесконечно велико. Обычно разница между прямым и обратным током диода настолько велика, что подобное допущение вполне справедливо.

Под действием переменного напряжения в цепи диода пойдет пульсирующий ток — импульсы тока будут появляться только тогда, когда переменное напряжение приложено к диоду в прямом направлении. Иными словами, ток будет протекать лишь в течение одной половины периода переменного напряжения. Отсюда и название схемы — однополупериодный выпрямитель.

Спектр получившегося пульсирующего тока содержит гармоники с частотами, кратными частоте повторения импульсов f 1 . Первая гармоника имеет частоту f 1 , вторая в два раза более высокую частоту f 2 = 2 f 1 третья частоту f 3 = 3 f 1 и так далее. Амплитуды гармоник постепенно убывают — вторая оказывается слабее первой, третья слабее второй, и т. д. С помощью резонансных фильтров все эти гармоники можно выделить из пульсирующего тока, точно так же, как, пустив весь набор гармоник в общую цепь, в итоге можно получить сигнал сложной формы.

Кроме гармоник, в получившемся пульсирующем токе I вып есть еще одна составляющая — постоянный ток I = . Появление этой постоянной составляющей связано с тем, что, хотя ток в цепи диода все время меняется, заряды толчками, импульсами двигаются всегда в одну сторону. Это постоянное смещение зарядов как раз и отображается постоянной составляющей I = . В то же время изменение тока, его пульсации отображаются всем набором гармоник.