Александр Гурштейн - Извечные тайны неба

Чтобы отличить друг от друга точки, лежащие на одном и том же меридиане, пришлось ввести вторую географическую координату – широту. Широтой называют угол, который проведенная в данном месте поверхности Земли отвесная линия образует с плоскостью экватора.

Термины «долгота» и «широта» дошли до нас от древних мореходов, которые описывали длину и ширину Средиземного моря. Та координата, которая соответствовала измерениям длины Средиземного моря, стала долготой, а та, которая соответствовала ширине, стала современной широтой.

Нахождение широты, как и определение направления меридиана, тесно связано с движением звезд. Уже древние астрономы доказали, что высота полюса мира над горизонтом hв точности равна широте места φ.

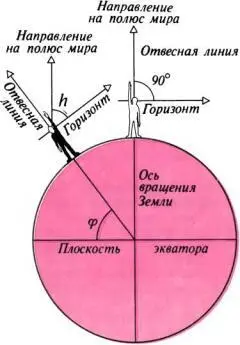
Предположим, что Земля имеет форму правильного шара, и рассечем ее по одному из меридианов, как показано на рисунке. Пусть на Северном полюсе стоит человек, изображенный на рисунке в виде светлой фигуры. Для него направление вверх, т. е. направление отвесной линии, совпадает с осью мира. Полюс мира находится у него прямо над головой. Высота полюса мира равна здесь 90°.

Так как видимое вращение звезд вокруг оси мира является отражением реального вращения Земли, то в любой точке Земли, как мы уже знаем, направление оси мира остается параллельным направлению оси вращения Земли. Направление же отвесной линии при переходе из точки в точку меняется.

Возьмем, например, другого человека (на рисунке темная фигура). Направление оси мира у него осталось таким же, как у первого. А направление отвесной линии изменилось. Поэтому высота полюса мира над горизонтом здесь не 90°, а значительно меньше.

Из простых геометрических соображений ясно, что высота полюса мира над горизонтом (на рисунке угол h) действительно равна широте (угол φ).

Линия, соединяющая точки с одинаковыми широтами, получила название параллели.

Меридианы и параллели образуют так называемую систему географических координат. Каждая точка на земной поверхности имеет вполне определенную долготу и широту. И наоборот, если известна широта и долгота, то можно построить одну параллель и один меридиан, в пересечении которых получится одна-единственная точка.

Понимание особенностей суточного движения звезд и введение системы географических координат позволили осуществить первое определение радиуса Земли. Оно было выполнено во второй половине III в. до н. э. известным математиком и географом Эратосфеном.

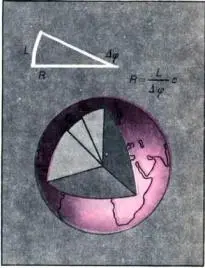
Принцип этого определения заключается в следующем. Пусть удалось измерить разность широт двух точек, лежащих на одном меридиане (см. рис.). Тем самым нам стал известен угол Δφ с вершиной в центре Земли, который соответствует дуге меридиана Lна поверхности Земли. Если теперь удастся измерить также и дугу L, то мы получим сектор с известной длиной дуги и соответствующим ей центральным углом. На рисунке этот сектор показан отдельно. Путем несложных вычислений можно получить величину радиуса этого сектора, который и является радиусом Земли.

Эратосфен, грек по национальности, жил в богатом египетском городе Александрии. Он был человеком разносторонне образованным, его увлекали подчас очень далекие друг от друга области науки. Друзья в шутку прозвали Эратосфена на спортивный манер «пятиборцем»: его не смущали трудности и, словно спортсмен, принимающий участие в пяти разных видах соревнований, Эратосфен для решения интересующей его задачи всегда готов был ринуться в любую новую область знаний.

К югу от Александрии находился другой город – Сиена, который в наши дни называется Асуаном и где, как известно, с помощью Советского Союза сооружена знаменитая высотная плотина. Эратосфен знал, что Сиена обладает интересной особенностью. В полдень одного из июньских дней Солнце над Сиеной бывает настолько высоко, что его отражение видно на дне даже очень глубоких колодцев. Отсюда Эратосфен заключил, что высота Солнца в Сиене в этот день равна точно 90°. Кроме того, раз Сиена лежит строго к югу от Александрии, то они находятся на одном меридиане.

Для необычного измерения Эратосфен решил воспользоваться скафисом – чашеобразными солнечными часами со штырьком и делениями внутри них. Установленные вертикально, эти солнечные часы по тени от штырька дают возможность измерить высоту Солнца над горизонтом. И в полдень того самого дня, когда Солнце над Сиеной поднялось настолько высоко, что все предметы перестали отбрасывать тени, Эратосфен измерил его высоту на городской площади Александрии.

Солнце в Александрии, по измерениям Эратосфена, отстояло от зенита на 1 / 50часть окружности. Стало быть, разность широт Александрии и Сиены в градусной мере составляет 7°12′.

Оставалось измерить расстояние между ними. Но как это сделать? Как измерить на поверхности Земли расстояние, равное в современных единицах примерно 800 км?

Трудности подобного предприятия были тогда буквально неисчислимы. Действительно, как изготовить такую гигантскую линейку, с помощью которой можно было бы произвести измерения? Как сделать, чтобы на протяжении 800 км эта линейка укладывалась строго по меридиану без всяких перекосов?

Но Эратрсфен недаром был выдающимся ученым. Его измерения высот Солнца отличались завидной точностью. Это легко проверить, поскольку он выполнял различные измерения. Так, например, он получил разность высот Солнца в одном и том же месте в день летнего и зимнего солнцестояний, равную 11/ 83частей круга, т. е. 47°43′; эта величина равна удвоенному углу между небесным экватором и эклиптикой и, как нетрудно убедиться по современным справочникам, получена с очень небольшой погрешностью. Предусмотрел Эратосфен и необходимость как можно более точно знать расстояние между Александрией и Сиеной.

Александрия и Сиена лежат в плодородной долине Нила, там, где исстари искусные шагатели-бематисты проводили тщательное межевание земель. Там же из года в год вереница за вереницей двигались навстречу друг другу торговые караваны. Расстояние между Александрией и Сиеной было известно в эпоху Эратосфена, пожалуй, гораздо более точно, чем расстояние между любыми другими отдаленными пунктами античного мира: оно составляло 5 тыс. греческих стадиев. Эратосфен принял это расстояние за истинное и, использовав его, вычислил радиус Земли.