Генрих Альтов - Творчество как точная наука. Теория решения изобретательских задач

Надо, однако, подчеркнуть, что таблица отнюдь не предназначена для решения «сырых» задач. Таблица - часть АРИЗ и должна быть использована совместно с другими его механизмами. В АРИЗ-77 применение таблицы - это шаг 4.4; сначала задача должна быть тщательно проанализирована.

Возьмем задачу 28. Даны два вещества: полый конус и шаблон (по правилу 4 в модели задачи должна быть одна пара), нет взаимодействия; задача относится к классу 4, как и задача о шлифовальном круге. Сходны до определенного момента и решения: в задаче о круге объект из твердого состояния был переведен в псевдожидкое (подвижный порошок); шаблон тоже можно сделать псевдожидким или просто жидким (нет центробежных сил, не надо думать о том, как удержать частицы). На этом, однако, сходство кончается, потому что задача о круге - на изменение, обработку, а задача о шаблонах - на измерение, обнаружение (зазоров между шаблоном и конусом). Теперь, когда анализ дал идею жидкого шаблона, легко притирающегося, но не приспособленного к измерениям, прием 26, подсказанный таблицей, приобретает точный смысл: надо снимать жидкий шаблон и сравнивать снимки с контрольным снимком. Конус ставят в ванну, наливают воду до определенного уровня и фиксируют уровень расположенным сверху фотоаппаратом. Затем доливают воду до следующего уровня и снова фотографируют на ту же пластинку. В результате на пластинке получается серия концентрических окружностей, которые легко сопоставить с окружностями на эталонном снимке (а. с. № 180 829).

Приемы подобны инструментам - сами по себе они не работают. Нужно потренироваться в их применении, порешать несколько десятков задач,

Для начала решите хотя бы четыре задачи.

Задача 42

Горячие газообразные нефтепродукты при движении по трубам образуют твердые парафиновые отложения. Приходится останавливать аппаратуру и удалять парафин растворителем. Предложено заранее насыщать газообразные нефтепродукты парами растворителя (а. с. № 412 230). Какой прием использован в этом изобретении?

Задача 43

Существуют дождевальные машины, которые разбрызгивают воду из поднятой над поверхностью земли и раскручиваемой трубы. Чем длиннее труба, тем большую площадь может полить такая машина. Но с увеличением длины трубы увеличивается ее вес, а это усложняет конструкцию машины, увеличивает расход энергии и т. д. Какой прием надо использовать, чтобы устранить это техническое противоречие?

Задача 44

Как было показано на многочисленных примерах, использование «мешка с воздухом» стало тривиальным при решении задач, в которых надо на время прижать один хрупкий предмет к другому. А если вместо «мешка с воздухом» взять антипод - «мешок с вакуумом»? Как он выглядит? Найдите изобретательское применение «мешку с вакуумом».

Задача 45

Во многих технических устройствах используются движущиеся ленты в виде бесконечного кольца. Если, например, покрыть внешнюю поверхность такой ленты абразивным составом, получится шлифовальная лента. В а. с. № 236 278 было предложено разрезать шлифовальную ленту, перекрутить один конец на 180° и снова соединить, получив так называемую ленту Мебиуса. Шлифующими стали обе поверхности ленты. Длина ее осталась той же, но и как бы вдвое увеличилась. Другие изобретатели проделали абсолютно тоже самое с магнитофонной лентой (а. с. №259449), ленточным фильтром (а. с. № 321 266), лентой станка для анодно-механической резки (а. с. № 464 429, девять авторов), конвейерной лентой (а. с. № 526 395) и десятками других лент. Какой прием здесь использован?

И еще один вопрос. Лента Мебиуса удваивает длину используемой поверхности. Но можно взять трехгранный шлифовальный ремень и перед соединением в кольцо сдвинуть концы на 120°. Тогда рабочая поверхность удлинится втрое (правда, став более узкой). Можно перекрутить многогранный ремень и удлинить поверхность в пять или десять раз. Но это изобретение выдано а. с. № 324 137. Спрогнозируйте изобретения, которые могут появиться в связи с этим авторским свидетельством.

Основные приемы и таблицы их применения - пожалуй, самое простое в АРИЗ. Применение приемов не требует той дисциплины мысли, которая необходима для анализа (вепольного и «по шагам»), не требует знания физики. Таблица привлекает автоматизмом: не надо думать, взял исходные данные и получил почти готовый ответ. За нынешней маленькой таблицей и коротким списком приемов оптимисты видят множество больших таблиц и длинные списки приемов, а отсюда уже рукой подать до применения ЭВМ...

После публикации АРИЗ-71 появилось много предложений по усовершенствованию фонда основных приемов. Так, В. Д. Воронков предложил «переделать» изобретательские приемы в организационные, предназначенные для решения общих задач управления и организации [21]. Л. С. Гуткин дополнил список специальными (радиотехническими) приемами [22]. А. И. Половинкин разделил приемы на множество подприемов [23.] Такого рода попытки предпринимаются с самыми лучшими намерениями, но, к сожалению, на чисто волевых основах. Единственный путь совершенствования фонда приемов - анализ больших массивов патентной информации, относящейся к изобретениям высших уровней. Путь этот трудоемкий, но стоило бы проанализировать несколько соток тысяч изобретений, чтобы в конце концов получить «большую таблицу и длинный список», если бы они гарантировали решение трудных задач. Дело, однако, обстоит значительно сложнее.

АРИЗ-68 включал список в 35 приемов, причем было проанализировано 25 тыс. патентов и авторских свидетельств. При подготовке АРИЗ-71 число проанализированных изобретений увеличилось на 15 тыс., а список приемов пополнился только пятью новыми приемами.

Прежде чем механически продолжать анализ, «выскребывая дно котла», следует разобраться в природе уже выявленных 40 приемов. Какие из них сильные и какие слабые? Почему одни приемы сильнее других? Нельзя ли вести целенаправленный поиск новых сильных приемов?

Обычно исследователи отождествляли силу приема с частотой его применения. На самом деле это разные понятия, и, оценивая эффективность того или иного приема, надо принимать во внимание оба фактора. Впервые такое исследование провела Д. М. Хитеева. Взяв большой массив патентной информации, она прежде всего отсеяла изобретения первого уровня, оставшиеся изобретения разделила на 40 видов (по числу приемов), а внутри каждого вида- на три группы: 2-, 3-й и 4 - 5-й уровни. Затем для каждого вида (т. е. для каждого приема) был подсчитан коэффициент эффективности К по формуле

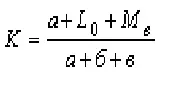
где а - количество изобретений, относящихся к первой группе (2-й уровень); б - количество изобретений, относящихся ко второй группе (З-й уровень); в - количество изобретений, относящихся к третьей группе (4 - 5-й уровни); L и M -коэффициенты, характеризующие качественные отличия изобретения второй и третьей групп по сравнению с изобретениями первой группы.