Валентин Красник - Управление электрохозяйством предприятий

3 – годовые условные потери, 3 = const.

Второй сомножитель в формуле (26) представляет собой среднюю стоимость отказов.

Для определения связи параметра безотказной работы электродвигателей с дополнительными капитальными вложениями априори можно принять, что последние являются функцией отношения параметров, т. е.

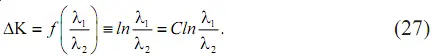
Из уравнения (27) видно, что дополнительные капитальные затраты пропорциональны уровню безотказности работы электродвигателей, т. е. возрастают (снижаются) при его повышении (снижении), что и выражено приемлемой для данного случая логарифмической функцией

С = const,

где С – параметр, определяющий постоянную затрат на повышение безотказности работы электродвигателей.

Этот параметр численно равен приращению стоимости объекта при уменьшении интенсивности отказов в e раз (2,71 раз).

Окончательно дополнительный экономический эффект AU от повышения уровня безотказности работы электродвигателей, приведенный к одной размерности, руб., можно представить как

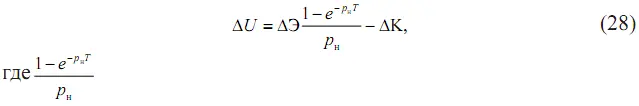
– показатель времени, характеризующий какой-то приведенныи момент времени T пр, произведение которого на значение эффекта и позволит получить приведенный эффект Δ U;

р н– нормативный коэффициент эффективности дополнительных капитальных вложений, значение которого обратно нормативному времени окупаемости, т. е. 1/6,7 = 0,15.

С увеличением срока службы Т электродвигателей приведенный момент времени стремится к 1/ р н , что дает основание судить об ограниченном значении приведенного эффекта.

С учетом формул (26) и (27) можно получить математическую зависимость дополнительного экономического эффекта:

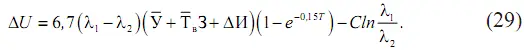
По уравнению (29) можно определить оптимальный уровень безотказности работы электродвигателей, который и принимают за максимум дополнительного экономического эффекта:

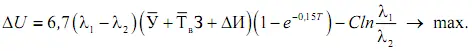
Для определения оптимальной интенсивности отказов уравнение (29) следует продифференцировать по Х 2 с последующим приравниванием производной нулю:

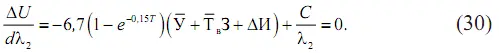
Следовательно,

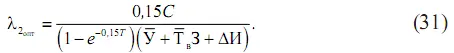
Из этой формулы видно, что оптимальное значение интенсивности отказов λ 2оптэлектродвигателей не зависит от начального значения λ 1и определяется только отношением постоянной затрат к средней стоимости отказа.

Если значение λ 2оптподставить в формулу (29), то после несложных преобразований можно определить максимальный экономический эффект, полученный за счет повышения уровня безотказности работы электродвигателей, и необходимые для этих целей капитальные вложения (см. вычитаемые в формулах (29) и (32)):

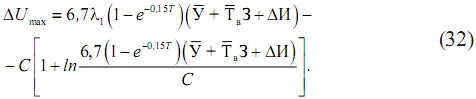
Если оптимальная интенсивность отказов λ 2оптне зависит от начального значения интенсивности отказов λ 1электродвигателей, то максимальный экономический эффект уже существенно будет зависеть от λ 1, что видно из формул (29) и (30):

при λ 1= λ 2оптΔU max= 0;

при λ 1> λ 2оптΔU max> 0 и с увеличением разницы между λ 1и λ 2оптзначение ΔU возрастает;

при λ 1 < λ 2оптΔU max < 0, что означает отсутствие дополнительного эффекта и наличие ущерба из-за значительных затрат и низкой экономичности работы электродвигателей.

Из уравнения (30) также видно, что максимальный экономический эффект зависит от исходного уровня интенсивности отказов λ 1и срока службы электродвигателей, и функционально может быть выражен следующей зависимостью:

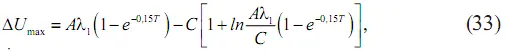
где постоянная A = 6,7 (У + Т в З + ΔИ).

В общем виде зависимость дополнительного экономического эффекта AU от начального значения интенсивности отказов X 1и времени T на основании формулы (29) можно выразить как

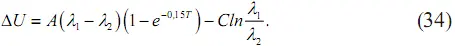
Следовательно, формула (33) есть частный случай формулы (34) для одной лишь точки функции, соответствующей оптимальному уровню безотказности работы эксплуатируемых электродвигателей λ 2опт.

С учетом постоянной А получим, что

Задавшись исходными значениями постоянных А, С и λ 2, построим график функции

ΔU = f(λ 2 , T).

В качестве примера возьмем данные отказов 300 асинхронных двигателей типа AOT 63-4 номинальной мощностью 10 кВт для привода прядильных и крутильных машин.

Априори примем следующие средние значения постоянных:

А = 5-10 7; С = 10; I 1= 4-10 -5при T = 0 .

Годовое значение числа часов работы T = 6000 ч для 3-сменных предприятий.

В результате получим

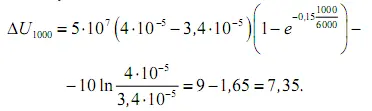
Следует отметить, что вычитаемое 1,65 представляет собой дополнительные капиталовложения. Определим

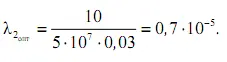
Используя формулу (34), в которой принимаем λ 2опт , или (33), получим значение максимального экономического эффекта: по формуле (34)

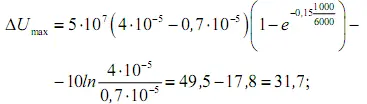
по формуле (33)

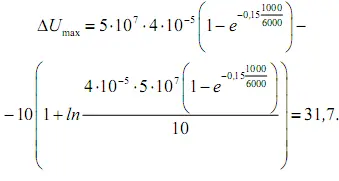
В табл. 5 приведены расчетные данные для построения взаимосвязанных графиков функций λ 2, λ 2опт, ΔU, ΔU max, ΔK maxи ΔK.

На рис. 7 показаны графики взаимосвязанных зависимостей всех величин, приведенных в табл. 5.

Из данных табл. 5 и графиков рис. 7 видно, что со снижением интенсивности отказов дополнительный экономический эффект монотонно возрастает и достигает максимума при λ 2опт.

Таблица 5

Расчетные данные для построения взаимосвязанных графиков функцийλ 2 , λ 2опт , ΔU, ΔU max , ΔK и ΔK max