Сергей Семиков - Баллистическая теория Ритца и картина мироздания

Итак, основу БТР составляет баллистический принцип, гласящий, что скорость света, и несущих его частиц (реонов), складывается со скоростью источника, подобно тому, как движение орудия придаёт дополнительную скорость выстреленному снаряду. Но до сих пор мы рассматривали лишь равномерное движение источника, относительно которого скорость света всегда имела постоянную величину c . Теперь изучим и случай ускоренно движущегося источника (относительно него скорость света равна c лишь в момент испускания). Для этого обратимся снова к баллистической модели. Представим себе идущий в атаку с ускорением a броневик, дающий очередь из пулемёта по неподвижной цели, расположенной прямо по курсу (Рис. 24). Пули в очереди следуют друг за другом через равные интервалы времени T . Найдём, с каким периодом T' они ударяют в мишень.

Рис. 24. Броневик, идущий в атаку, даёт пулемётную очередь по цели. Пули, выстрелянные через период T, бьют в мишень с периодом T'.

Первая пуля долетит до цели за время

t 1=L 1/v 1 ,

где L 1 — расстояние до мишени, первоначально равное L (Рис. 25. а ), а v 1 — скорость пули, равная сумме стандартной скорости c вылета пуль из ствола пулемёта и скорости v броневика в этот момент:

t 1= L/(c+v) .

Следующая пуля прибудет к цели за время

t 2=T+L 2/v 2 ,

где T — время, прошедшее от первого выстрела до второго, а L 2/ v 2 — собственно время движения второй пули. Отрезок L 2 , который ей предстоит пройти, будет меньше L на величину пройденного броневиком за время T пути, равного vT , то есть

L 2= L-vT (Рис. 25. б ).

Иной окажется и скорость пули v 2 . Броневик движется ускоренно, и спустя время T скорость его будет на величину aT больше первоначальной. И настолько же скорость второй пули будет превышать v 1 , т. е.

v 2= v 1+aT= c+v+aT.

В итоге имеем

t 2= T+((L-vT)/(c+v+aT))

Промежуток времени T΄= t 2-t 1 между двумя ударами пуль в мишень найдётся как

T' = T(1-v/(c+v+aT)-La/((c+v+aT)(c+v)))

Считая малыми в знаменателях величины v и aT (в сравнении со скоростью выброса пуль c ), получим T΄/T=1-ν/c-La/c 2 , или то же для частот ( f =1/ T ):

f΄/f = 1+ ν / c+La / c 2.

То есть пули по мишени барабанят чаще (с частотой f΄ > f ), чем вылетают: движение как бы добавляет пулемёту скорострельности.

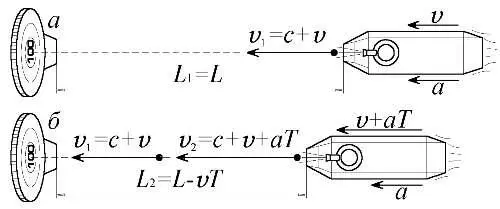
Рис. 25. Положения и скорости пуль, броневика вначале и спустя время T.

Применяя баллистическую модель к свету (броневик — это источник света, а пули — реоны R , соответствующие гребням волн и "выстреливаемые" со скоростью света c ), получим тот же результат: видимая частота прихода световых волн, импульсов от подвижного источника отличается от истинной.

Здесь, конечно, нет никакого реального искажения масштаба времени, как в теории относительности. Имеет место лишь кажущееся изменение, как в общеизвестном эффекте Доплера (Рис. 26). К нему и сведётся найденная формула в случае равномерного движения источника ( a= 0). Именно эффект Доплера T ΄ /T =1- ν / c используют автоинспекторы для определения скорости ν движения автомобилей. Неподвижному наблюдателю с чувствительной аппаратурой свет фар приближающейся машины покажется чуть синее, чем в действительности [76]. Если же машина уносится прочь, свет её задних фар, напротив, станет казаться чуть красней реального: движение меняет частоту света. Вызвано это тем, что при движении расстояние между машиной и наблюдателем меняется. Поэтому два последовательных сигнала, скажем, — два выстрела из автомобиля, произведённые с интервалом в секунду, пройдут это расстояние в разное время (Рис. 27). Так, при стрельбе из машины, идущей к наблюдателю со скоростью 30 м/с, второй пуле предстоит пролететь на 30 метров меньше. Поэтому, при скорости пуль в 300 м/с вторая пуля выиграет на этой дистанции десятую долю секунды. На эту разность времён хода и сократится для наблюдателя период между сигналами: пули проследуют с интервалом в 0,9 секунды, вместо 1 с. Так же и для света, представляющего собой летящую последовательность волновых фронтов, движение преобразует период и частоту следования импульсов, гребней волн, то есть, — меняет окрашенность света по эффекту Доплера. Но формула, найденная Ритцем ещё в 1908 г. [8], предсказывает, помимо доплеровского, и другой эффект.

Рис. 26. Эффект Доплера — изменение частоты света за счёт движения.

В самом деле, пусть начальная скорость ν ускоряемого источника света равна нулю. Тогда приходим к формуле для периодов

T΄/T =1- La / c 2,

или с учётом малости La / c 2<<1 получим для частот света f= 1/ T и f΄= 1/ T΄ соотношение

f΄/f= 1/( T΄/T ) = 1+ La / c 2.

То есть, даже при нулевой скорости, когда эффект Доплера не даёт никакого сдвига частоты, такой сдвиг частоты сигналов предсказывает формула Ритца (изменение частоты обусловлено повышенной скоростью задних гребней волн, сигналов: они нагоняют передние, постепенно сокращая разрыв, длину волны, Рис. 24). Пусть, для иллюстрации, этими сигналами снова будут два пистолетных выстрела из автомобиля по столбу. Первый выстрел производится из автомобиля, едва начавшего разгон и потому имеющего нулевую скорость. Тогда первая пуля двинется к столбу со стандартной скоростью выстрела c =300 м/с, пройдя расстояние L =900 м до столба за время L/c =3 секунды. Когда после первого выстрела, спустя время T= 1 с, будет произведён второй, машина, имеющая ускорение a= 10 м/с 2, наберёт уже скорость V=aT =10 м/с. Это движение автомобиль дополнительно сообщит второй пуле, так что её скорость составит уже c+V= 310 м/с, а время пути станет L/ ( c+V )=2,9 с, что примерно на величину LV/c 2=0,1 секунды меньше продолжительности полёта первой пули. Следовательно, к столбу пули придут с разрывом T' = T-LV/c 2= T (1 —La/c 2)=0,9 с, меньшим первоначального T= 1 с. Как видим, эффект во многом напоминает доплеровский, но в отличие от него определяется лишь ускорением источника a и нарастает с расстоянием L . По аналогии с эффектом Доплера назовём такой неизвестный науке способ влияния на частоту "эффектом Ритца" (Рис. 27).