Сергей Семиков - Баллистическая теория Ритца и картина мироздания

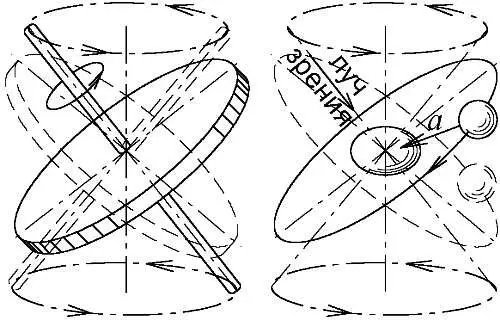
Рис. 77. Изменение наклона к лучу зрения плоскости волчка и звёздной орбиты.

Поскольку у звёзд, как у Луны, прецессионное вращение орбит цикличное (сделав полный оборот, орбита займёт прежнее положение), то и степень колебаний блеска цефеид должна меняется периодично. Особенно такие вариации характерны для звёзд типа RR Лиры и карликовых цефеид, — переменных с периодами в несколько часов. И не удивительно, ведь столь малый период обращения говорит о близости компонент двойной звезды и ощутимости гравитационного возмущения орбит. Не зря, у таких звёзд обнаружены и другие необъяснимые теорией пульсаций аномалии: периодично меняется форма кривой блеска (эффект Блажко) и очень медленно — период его колебаний [158]. Эти вариации легко объяснимы в БТР. В тесных двойных системах орбиты звёзд поворачиваются, подобно перигелию орбиты Меркурия (§ 2.3), только гораздо быстрее. Впервые такое явление постепенного смещения периастра двойных звёзд обнаружил всё тот же Белопольский [17]. По мере вращения орбиты, меняется, в зависимости от угла поворота, — форма кривой ускорений (Рис. 68) и, соответственно, — форма кривой блеска (Рис. 78). Когда орбита сделает полный оборот, кривая блеска примет исходную форму. То есть, в полном соответствии с эффектом Блажко, вариации кривой должны периодично повторяться.

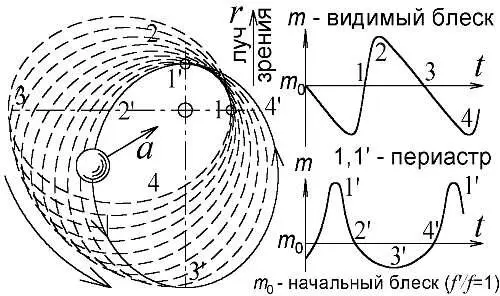
Рис. 78. Поворот звёздной орбиты меняет форму кривой ускорения a rи блеска m.

Теперь о причинах плавного изменения периода цефеид. Здесь снова дело в приливных гравитационных силах, под действием которых орбиты звёзд в тесных двойных системах постепенно расширяются (такой эффект реально выявлен астрономами у короткопериодических двойных звёзд и у Луны, которая, постепенно отдаляясь от нас, увеличивает продолжительность месяца [28]). Соответственно, нарастает орбитальный период и равный ему период колебаний блеска. У той же Полярной период ежегодно увеличивается на 8 секунд. Как видим, Полярная — весьма интересный и даже ключевой объект ("Природа" 2005, № 7), — не только как звезда с северного полюса мира и ближайшая к нам цефеида, но и как одно из главных подтверждений гипотезы Белопольского о двойственности цефеид. Не зря, Полярная была "любимицей" Белопольского — предметом его пристального внимания [17, 51]. Именно Белопольский первым обнаружил, что Полярная входит в двойную систему, где второй компонент — карлик главной последовательности с периодом обращения в 30 лет. Однако, колебания блеска с периодом в 4 дня у Полярной, вероятно, вызваны более близким и невидимым спутником (звездой или планетой). Не исключено, впрочем, что именно орбитальное движение Полярной в системе карлика с нарастающим a r вызывает вековые вариации: постепенный рост видимого периода её мерцаний T΄ = T (1+ La r / c 2), с медленным падением средней яркости пропорционально T΄/T , по эффекту Ритца. Точно так же, ритц-эффект может плавно наращивать или снижать период миганий и у других цефеид и переменных звёзд, входящих в кратные системы.

Иногда, вместо плавных, наблюдаются скачкообразные изменения периодов цефеид, невозможные в ТП [158]. Зато, если цефеиды — двойные, такие сдвиги периода вполне могут быть вызваны столкновением звезды с малым космическим телом. Удар скачком меняет скорость звезды, её орбиту и период обращения, но, за счёт малой массы врезавшегося тела, это изменение периода обычно мало в сравнении с самим периодом. Таким образом, все странные пертурбации мигающих звёзд — это следствие изменения размера, формы, наклона и поворота их орбит.

К слову о периоде, БТР объясняет и знаменитую зависимость период-светимость: чем выше период колебаний блеска звезды, тем выше её абсолютная яркость. Связь "период-светимость" и сделала цефеиды маяками космоса: определив по периоду действительную яркость цефеиды и, сравнив с видимой, находят удалённость звезды. Но почему же период выше у ярких цефеид? Причина в том, что цефеиды — это очень тесные системы, где размеры звёзд и их орбит сопоставимы. Поэтому, более крупные и яркие цефеиды и орбиты имеют большие, а, значит, — и периоды. А вот для звёзд типов Миры Кита и RV Тельца, имеющих периоды около года и широкие орбиты, основное значение приобретает уже масса звезды. Поэтому, чем ярче, массивней звёзда, тем быстрей крутятся возле неё спутники, и тем меньше период миганий. Недаром, у звёзд указанных типов зависимость "период-светимость" — обратная в сравнении с цефеидами: чем выше период, тем меньше яркость [158], о чём в теории пульсаций упоминать не любят, поскольку не могут объяснить.

Используя ТП, нельзя объяснить даже форму кривых блеска. У цефеид и звёзд типа RR Лиры эти кривые часто имеют отчётливый горбик (Рис. 75) — вторичный максимум [157]. Истолковать его можно, лишь считая цефеиды двойными. Обычно, у двойных звёзд, образующих цефеиды, заметна лишь главная, более яркая звезда, тогда как блеск звезды-спутника, или, даже, — планеты, совершенно незаметен на её фоне, что предполагал ещё Белопольский [51]. Но, в случаях, когда яркость главной звезды и спутника сопоставимы, их кривые блеска, слагаясь, дадут два максимума и минимума (Рис. 79). Существованием двух колебаний, наложенных и сдвинутых по фазе, объясняют вторичный максимум и в теории пульсаций, но не могут объяснить, откуда берётся сдвинутое по фазе колебание [102, с. 89]. А БТР объясняет не только этот фазовый сдвиг (лучевые ускорения пары звёзд колеблются в противофазе), но и его изменение: смещение горбика в зависимости от периода цефеиды [157, 158]. Просто положения максимумов на кривых блеска главной звезды и звезды-спутника зависят от их орбитальной скорости, а, значит, — от периода их обращения. Тот же эффект вторичного максимума может создать и одна звезда. Ведь кривая ускорений, как показывает компьютерное моделирование, имеет плавную форму лишь у звёзд с орбитами малого эксцентриситета ε. При ε=0,3 и более на кривой ускорений возникает горбик (Рис. 75), переходящий и на кривую блеска. Причём, моделирующая программа позволяет наблюдать постепенное смещение вторичного максимума по кривой блеска — при увеличении периода цефеиды, в полном согласии с наблюдениями. Но, несмотря на успехи БТР в разгадке форм кривых блеска цефеид, эффекта Блажко и других закономерностей и аномалий, некоторые авторы [82] ещё пытаются нас убедить, что характер колебаний яркости цефеид не совпадает с предсказаниями баллистической теории. На деле же, такие нестыковки всегда отличали как раз пульсационную теорию цефеид Эддингтона.