Лоуренс Краусс - Всё из ничего [litres]

В классической механике, как я и описываю, определение потенциальной энергии произвольно. Я мог бы принять равной нулю потенциальную энергию тела на поверхности Земли, и тогда на бесконечно далеком расстоянии она бы стремилась к какому-то очень большому числу. Решение приравнять к нулю общую энергию на бесконечности имеет физический смысл, однако это всего лишь вопрос договоренности, по крайней мере на нынешнем этапе нашего повествования.

Вне зависимости от того, где мы назначим точку нуля потенциальной энергии, у всех тел, подверженных только силе гравитации, есть одно чудесное свойство: сумма их потенциальной и кинетической энергии остается постоянной. При падении тела потенциальная энергия переходит в кинетическую энергию движения, а когда тело отскакивает от Земли, кинетическая энергия переходит в потенциальную, и т. д.

Это дает нам восхитительный бухгалтерский инструмент, позволяющий определять, с какой скоростью нужно запустить тело в воздух, чтобы оно улетело от Земли, поскольку, если оно в конечном итоге должно уйти на бесконечное расстояние от Земли, его общая энергия должна быть больше или равна нулю. Тогда мне остается просто сделать так, чтобы полная гравитационная энергия тела в момент, когда оно оторвется от моей руки, была больше или равна нулю. Поскольку я контролирую только одну составляющую полной энергии – скорость, с которой тело оторвется от моей руки, мне нужно всего-навсего рассчитать ту волшебную скорость, при которой положительная кинетическая энергия мяча равняется отрицательной потенциальной энергии, которую дает ему притяжение на поверхности Земли. И кинетическая, и потенциальная энергия мяча одинаковым образом зависят от массы мяча, которая, таким образом, сокращается при приравнивании этих двух величин, поэтому «скорость убегания» от земной поверхности, она же вторая космическая скорость, для всех тел в природе одинакова и составляет около 11 км/с. Как раз в этом случае полная гравитационная энергия тела в точности равна нулю.

Тут вы вправе задать вопрос, какое все это имеет отношение ко Вселенной в целом и к инфляции в частности. Дело в том, что расчеты для мячика, который я бросаю рукой у земной поверхности, применимы к любому телу, любому объекту в нашей расширяющейся Вселенной.

Рассмотрим сферическую область Вселенной с центром там, где находимся мы с вами (в галактике Млечный Путь), такого размера, чтобы в нее входило достаточно много галактик, но не слишком большую, чтобы она вполне укладывалась в пределы расстояний, на которых мы можем сегодня вести наблюдения.

Если эта область достаточно велика, но не слишком огромна, то галактики на ее краю будут равномерно удаляться от нас в соответствии с хаббловским расширением со скоростью, гораздо меньшей скорости света. В этом случае к ним применимы законы Ньютона, а эффектами общей и специальной теории относительности можно пренебречь. Иначе говоря, каждый объект подчиняется точно таким же законам физики, что и мячик, который я пытаюсь зашвырнуть в космос.

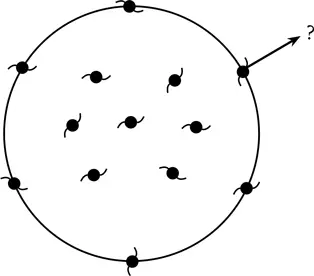
Рассмотрим галактику, которая движется от центра выбранной области, как изображено на рисунке. Как и в случае с мячиком, который бросают с Земли, можно задаться вопросом, сумеет ли галактика преодолеть гравитацию всех остальных галактик в сфере. Чтобы получить ответ, нам надо проделать те же самые вычисления, что и для мячика. Мы попросту подсчитываем полную гравитационную энергию галактики, учитывая ее движение наружу (что дает положительную энергию), и гравитационное притяжение ее соседок (что дает отрицательное слагаемое энергии).

Если полная энергия галактики больше нуля, она умчится в бесконечность, а если меньше, остановится и начнет падать внутрь сферы.

И вот что интересно: вполне можно переписать простую формулу Ньютона для полной гравитационной энергии этой галактики таким образом, что она в точности повторит уравнение Эйнштейна из ОТО для расширяющейся Вселенной. Тот член уравнения, который соответствует полной гравитационной энергии галактики, в ОТО становится членом, который описывает кривизну Вселенной.

Так что же мы тогда найдем? В плоской Вселенной, и только в ней, суммарная средняя ньютоновская энергия гравитации каждого объекта, который движется в рамках расширения Вселенной, в точности равна нулю!

Именно поэтому плоская Вселенная – совершенно особый случай. В такой Вселенной положительная энергия движения в точности уравновешена отрицательной энергией гравитационного притяжения.

Если мы начнем все усложнять и допустим, что пустое пространство обладает энергией, то простая ньютоновская аналогия с подбрасыванием мячика в воздух становится некорректной, но вывод остается, в сущности, прежним. В плоской Вселенной, даже если в ней есть небольшая космологическая постоянная, на масштабе, который достаточно мал, чтобы скорости оставались гораздо меньшими скорости света, Ньютонова гравитационная энергия, связанная с каждым телом во Вселенной, равна нулю.

Более того, в присутствии энергии вакуума «бесплатный обед» Алана Гута становится еще вкуснее. По мере того как каждая область Вселенной расширяется и набирает объем, она становится все более и более плоской, поэтому полная Ньютонова гравитационная энергия всего, что получится после того, как энергия вакуума в процессе инфляции преобразуется в вещество и излучение, в точности равна нулю.

Но вы все равно имеете полное право спросить: откуда берется вся энергия, благодаря которой плотность энергии остается постоянной в процессе инфляции, когда Вселенная расширяется экспоненциально? Тут на помощь приходит еще одна интересная особенность ОТО. Отрицательной может быть не только гравитационная энергия объектов, но и их релятивистское «давление».

Вообразить отрицательное давление даже труднее, чем отрицательную энергию. Газ – скажем, в воздушном шаре – давит на стенки шара. Если он расширяет стенки шара, то совершает над ним работу. Эта работа заставляет газ терять энергию и охлаждаться. Однако оказывается, что энергия пустого пространства потому и имеет вид гравитационного отталкивания, что заставляет пустое пространство иметь «отрицательное» давление. В результате отрицательного давления Вселенная при расширении совершает работу над пустым пространством. Эта работа позволяет поддерживать постоянную плотность энергии даже при расширении Вселенной.

Таким образом, если квантовые свойства вещества и излучения в конечном итоге обеспечили энергией даже самые крошечные области пустого пространства на самых ранних этапах существования Вселенной, эти области, расширяясь, могли стать сколь угодно большими и сколь угодно плоскими. Когда инфляция заканчивается, может получиться Вселенная, набитая всякой всячиной (веществом и излучением), причем общая Ньютонова гравитационная энергия этой всячины будет так близка к нулю, что ближе и представить себе невозможно.