Генрих Альтшуллер - Крылья для Икара. Как решать изобретательские задачи

Задача 8. При выплавке чугуна в домнах образуется расплавленный шлак (смесь окислов алюминия, магния, кальция и др., температура около 1000°), который сливают в ковши и увозят на шлакоперерабатывающие установки. Шлак, залитый в ковш, охлаждается, на его поверхности появляется твердая корка. Чтобы вылить шлак из ковша, в корке с помощью специального копрового устройства пробивают два отверстия. Однако отверстия эти приходится делать не у стенки ковша, поэтому часть шлака остается в ковше. Пробивать отверстия в корке у самых стенок ковша по ряду причин невозможно (ковши по-разному наполняются шлаком, корка имеет разную толщину, стенки ковша — конусные и т. д.). Это отпадает.

Основное охлаждение происходит с открытой поверхности шлака. Но закрыть ковш теплоизолирующей крышкой затруднительно, поскольку потребуются громоздкие устройства для открывания и закрывания ковша.

Затвердевание шлака в ковше и неполный слив приводят к тому, что примерно одна треть шлака не используется на шлакоперерабатывающих установках. Приходится сооружать специальные эстакады: там выбивают затвердевший в ковшах шлак, сливают остатки жидкого шлака, охлаждают водой и самосвалами вывозят в отвалы, громоздящиеся вокруг заводов.

Возникает задача: как обеспечить полный слив жидкого шлака?

Как видите, разобраться в условиях задачи очень просто. Есть большие металлические «банки» (ковши), в которых возят расплавленный шлак. Нужно свести до минимума потери жидкого шлака и сделать это без усложнения оборудования.

1. Запишите возможные варианты решения. Постарайтесь, чтобы их было не меньше десятка.

2. Зачеркните все варианты, требующие хотя бы небольшого переустройства оборудования.

3. Предложите эту задачу своим друзьям. Желательно, чтобы 5—6 человек записали свои варианты. Сколько разных вариантов получилось? Сколько разных вариантов останется, если зачеркнуть варианты, требующие переустройства оборудования?

Сохраните записи. Мы еще вернемся к этой задаче.

* * *

Теперь мы знаем: изобретательские задачи имеют разную «цену». Есть задачи «ценой» всего в несколько проб, решение таких задач доступно каждому, и есть задачи, решение которых приходится оплачивать многими тысячами проб. Творчество проявляется именно в решении «дорогостоящих» задач. Если бы удалось найти прием, позволяющий делать «дорогостоящую» задачу общедоступной, мы могли бы считать, что тайна творчества раскрыта.

Нечто подобное описано в фантастическом рассказе Рэймонда Джоунса «Уровень шума». Использован прием (всего лишь один прием!): при помощи хорошо разыгранного спектакля с кинотрюком психологи убедили ученых в возможности существования антигравитации — и удалось решить труднейшую задачу и построить антигравитационный летательный аппарат. Вот концовка рассказа. Психолог Бэрк говорит физику Марту:

«...Мы расшатали ваши умственные фильтры, и в результате появился ответ. Метод сработал, он будет действенным всегда. Все, что необходимо сделать, это избавиться от лишнего груза предрассудков, от окаменевшего мусора в голове, изменить произврльную настройку ваших умственных фильтров в отношении других вещей, которые вам всегда хотелось сделать, и тогда удастся найти нужный ответ на любую проблему, какую вы только пожелаете исследовать.

Март взглянул на небо.

— Да, вот они, звезды, — сказал он. — Я всегда хотел добраться до зьезд. Теперь, когда у нас есть антигравитация...

— Вы можете полететь к звездам, если заходите.

Март покачал головой.

— Вы и Даннинг. Вы заставили нас создать антигравитацню. И это становится совсем простым делом. Конечно, мы смогли бы побывать на планетах, может быть, даже слетать за пределы солнечной системы. Но я думаю, что останусь здесь и буду работать с вами. Одна или две жалкие планеты — чего это стоит в конце концов. Но если мы научимся использовать максимальный уровень шума человеческого ума, мы сможем покорить всю вселенную!»

Что ж, значение проблемы показано верно. Человек познает и покоряет вселенную, решая творческие задачи. Если в сотни раз увеличить число людей, умеющих решать творческие задачи,— темпы прогресса возрастут тысячекратно. Но существует ли прием, позволяющий произвольно изменять «настройку умственных фильтров»? Вот в чем вопрос...

ИНСТРУМЕНТЫ ЕСТЬ, НО...

Наверное, нет игрушки проще, чем кубики. Сложил квадрат или прямоугольник из кубиков — получился рисунок. Повернул кубики — другой рисунок. Снова повернул — еще один рисунок... Игрушка настолько простая, что мы легко осваиваем ее, едва

вступив в детсадовский возраст. Осваиваем... и бросаем: слишком уж она проста. А если приспособить кубики для решения изобретательских задач? Давайте подумаем. Кубики образуют рисунок, допустим, рисунок машины или прибора. Мы переворачиваем кубики — возникает другой рисунок: совершенно новая машина или новый прибор, никому еще не известное изобретение... Невозможно? Что ж, проверим!

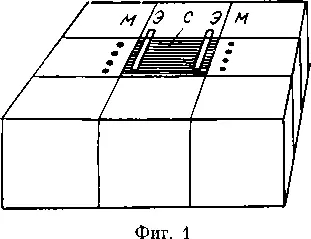
Нарисуем, например, на кубиках схему электромагнитного расходомера (фиг. 1). Это простой прибор, состоящий из металлических электродов Э и магнитной системы М. Электроды опущены в жидкую электропроводящую среду С (раствор кислоты, щелочи, соли), движущуюся по лотку или по трубе. Как известно, при движении проводника в магнитном поле возникает электрический ток: на электродах, опущенных в движущуюся жидкость, наводится электродвижущая сила, которую легко измерить гальванометром. Чем выше скорость потока жидкости, тем сильнее отклоняется стрелка гальванометра. Зная скорость потока и площадь его поперечного сечения, нетрудно определить, сколько жидкости прошло по трубопроводу за то или иное время.

Итак, на картинке — расходомер. Если бы теперь повернуть кубики и получить схему какого-то нового прибора! Но другие грани кубиков пока пусты. Сколько бы мы ни переворачивали кубики, нового изобретения не будет. Есть, однако, простой выход. У расходомера три основные части, причем расположены они в определенном порядке. Снаружи — с двух сторон — магнитная система М, внутри два электрода Э, а в самой середине—среда С:

МЭСЭМ

Для симметрии запишем С два раза (ведь другие буквы встречаются в этой записи по два раза):

МЭССЭМ

Возьмем теперь шесть кубиков. Пусть на каждом кубике будет только одна буква — М, Э или С. Расположим кубики в линию и начнем их перекладывать. Получится шесть симметричных комбинаций:

1. МЭССЭМ

2. ЭМССМЭ

3. СМЭЭМС

4. МСЭЭСМ

5. ЭСММСЭ

6. СЭММЭС

Первая формула соответствует уже знакомому нам электромагнитному расходомеру. А другие пять? По-видимому, это тоже расходомеры, у них те же основные части — поток жидкости, электроды, магнитная система. Но это уже какие-то другие расходомеры, необычные. Например, в конструкциях 3 и 6 жидкость находится снаружи.