Иван Ефишов - Таинственные страницы. Занимательная криптография

В июле 1766 года Эйлер уже навсегда вернулся в Россию.

В 1907 году, когда отмечалось двухсотлетие со дня рождения Л. Эйлера, математик Фердинанд Рудио, будучи президентом Эйлеровского комитета в Базеле, объявил о состязании и назначил награду за решение приведенного выше логогрифа {35}. Как видим, прошло 163 года со дня написания письма, а криптограмма все еще надежно хранила свою тайну. Увы, пришлось повторно объявлять награду за разгадку этой головоломки в 1953 году. Вскоре элегантное решение было найдено Пьером Специали {36}.

Прежде чем давать читателю подсказки и облегчить ему тем самым последующую самостоятельную работу, проследим немного за мыслью Специали (используя для этого его публикацию).

Каким же образом ему удалось разрешить эту криптограмму через двести с небольшим лет после ее создания?

В своем письме Эйлер сразу дает нам три ценные подсказки:

• текст на латинском языке;

• каждый символ (знак) сохраняет один и тот же смысл во всем сообщении;

• все символы имеют значение (то есть нет символов-пустышек).

Определимся с терминологией. Назовем частотой число, показывающее, сколько раз символ встречается в тексте; относительная частота подсчитывает то же самое, но в процентном выражении.

Расставим буквы латинского алфавита [31]согласно порядку убывания их относительных частот в латинском языке: [32]

Табл. 1. Относительная частота букв латинского алфавита в произвольном тексте, %

Естественно, если взять разные тексты, то возможны незначительные вариации этих цифр. Так, было исследовано литературное наследие Гая Юлия Цезаря (на основе 52 тысяч слов), и порядок букв там немного другой [33]:

E I T U A S R N O M C P L D Q B G V F H X Y K Z.

Как видим, самая редкая буква латинского языка – k , она используется лишь в нескольких словах, например, kalendae (календы). Это связано с тем, что звук «к» в основном передавался буквами c и q.

Если бы Эйлер предупредил нас, например, что это отрывок из сочинений Цезаря, то мы бы попытались поискать в криптограмме слова, которые часто употребляли тогдашние военные: bellum (война), gallus (галл), hostis (враг), pugnare (борьба), scorpione (маленькая катапульта, стреляющая железными дротиками) и т. п. Решение головоломки значительно упростилось бы. Конечно, тогда бы при дешифровке мы пользовались не табл. 1, а порядком букв в сочинениях Цезаря.

А если, например, мы бы точно знали, что перед нами текст латинской мессы (службы) римско-католического богослужения, то все бы радикально изменилось. Нам бы не составило труда узнать, что первые слова этой службы – Kyrie eleison («Господи, помилуй»), и дело бы сразу сдвинулось с мертвой точки.

Интересно отметить, что здесь частотный ряд букв сильно изменился бы (начальные слова службы многократно повторяются), так как слово «Господи» начинается с самых редких букв латыни k и y . Это связано с тем, что данные слова заимствованы из греческого языка (Κύριε ελέησον).

Но ученый был достаточно осторожен, чтобы не облегчать таким образом решение задачи, и ни словом не намекнул на содержание зашифрованного текста.

Cделаем статистический анализ символов логогрифа (в дальнейшем будем использовать строчные буквы для шифра и прописные для латинского алфавита), в котором содержится 408 знаков.

Табл. 2. Статистический анализ символов логогрифа Эйлера в порядке убывания их частот

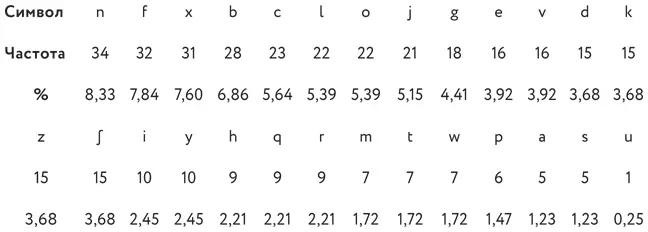
Первое наблюдение, которое сделал Специали: загадка содержит 26 букв современного английского алфавита и знак ∫ (вытянутая буква s ). Но классический латинский алфавит имеет только 23 буквы. Пять наиболее частых I, E, A, U, T – это примерно половина (48,17 %) любого латинского текста. В нашей криптограмме, в которой 408 знаков, каждая из этих букв должна появиться примерно по 40 раз. Самый частый у нас символ n , но и он встречается «всего лишь» 34 раза. По-видимому, это означает, что Эйлер использовал по крайней мере два представления (называемых омофонами) для самых частых букв. Изменяя таким образом частоты, ученый пытался сделать логогриф неуязвимым для частотного анализа. Как видим, Эйлер кое-что знал о простейших шифрах и методах их взлома. Логогриф Эйлера относится к шифрам многозначной замены (его также можно классифицировать с некоторыми оговорками и как омофонический шифр).

В случае омофонического шифра криптоаналитику следует попытаться получить максимум информации из сдвоенных символов (то есть один и тот же знак пишется в тексте два раза подряд) и отследить группы символов, их содержащие.

Разобьем логогриф на десятки символов для удобства исследования:

0: pxq∫w lznjd

1: vyn∫t iddkq

2: xhlee bfpxd

3: fgtlz bccfb

4: k∫odx okfng

5: lqxn∫ shejm

6: lckzx hrfwj

7: gfhxv zjnbg

8: yxcdg ixkox

9: jmlnc oigdx

10: vzflm e∫nfy

11: jqfan gvnyl

12: rcxfo nbfja

13: lrkw∫ nbfpj

14: oizox qknub

15: ro∫ad giaxw

16: kcbrb cklof

17: rnjwn g∫zfh

18: gjfcb cfvqj

19: txeev tbzfy

20: jsbzh ∫mlnb

21: g∫sqj wglnx

22: vzfko nbcoi

23: gdxvr kfjal

24: zxt∫n ilenf

25: gvcbo ofcfx

26: nnfgn kbcjn

27: njynx vplgn

28: bfzfo xeejd

29: gxbcj cn∫dy

30: vdbhz lnvyx

31: mbcbl obbcy

32: fekon bceio

33: bfplw sxzxf

34: jcndb hrlzq

35: xs∫on bcolj

36: f∫yqf mjeev

37: hleex oiexm

38: gicfd nktvo

39: ldxnf bxo∫c

40: ktvpx rnv

Сдвоенные символы позволяют различать гласные и согласные буквы. Вот они в порядке их следования в криптограмме (сдвоенные символы являются «каркасом» целой группы символов): iddk (с 16-й позиции в логогрифе; далее кратко будем писать просто 16), leeb (23), bccf (36), xeev (192), boof (254), xnnf (260), jnnj (269), xeej (286), obbc (316), jeev (367) и leex (372). Скорее всего, символы по краям каркаса представляют гласные, а именно: i, k, l, f, x, j, v . Внимательнее приглядимся к трем не перечисленным выше, но также «крайним» символам b, о, и с, которые одновременно являются и каркасными. Исключение из них составляет только b . Обратим на него внимание в группе obbc. Но ведь и о, и с образуют в следующих группах bccf, boof каркас, и здесь мы видим b также крайним символом; поэтому, думается, нет никакого риска в предположении, что символ b обозначает гласный звук. Остальные знаки, скорее всего, обозначают согласные: d, e, c, o, n .

Особый интерес представляет символ е . Он появляется целых пять раз сдвоенным (24, 193, 287, 368, 373) и шесть раз одиночным (58, 106, 248, 322, 328, 378). Буква, сама по себе достаточно редкая, однако часто удваиваемая в латыни, – это l (например, в словах aucella (птичка), bellum (война), cellа (каморка), mantellum (покрывало), nullum (ничто) и т. д.); можно просто взглянуть на любой латинский текст, чтобы убедиться в этом. Итак, сделаем предположение, что e – это буква L.