Сергей Титов - Естествознание. Базовый уровень. 10 класс

Слово «алгоритм» очень старое и происходит от имени аль– Хорезми, учёного, написавшего в IX в. сочинение, в котором разрабатывались правила некоторых математических вычислений. В современном понимании алгоритм – это совокупность операций и правил последовательных вычислений, которые в конечном счёте должны привести к определённому результату. Понятие алгоритма стало особенно широко применяться после изобретения вычислительных машин. Ведь, по существу, любая программа вычислений представляет собой алгоритм. Вот, например, простой алгоритм, который может быть выражен в виде компьютерной программы:

«Взять два числа – х и у, перемножить их, затем прибавить к произведению тройку и извлечь из получившейся суммы квадратный корень. Если значение корня окажется целым числом, выдать ответ, что введённые числа составляют пару для данной операции».

Такой алгоритм можно легко вычислить в уме. Нетрудно сообразить, что соответствующие этому условию пары составляют, например, числа 1 и 6; 2 и 3; 2 и 11 и бесконечное количество других.

Создание модели обычно включает определённые этапы. Вначале происходит словесное, качественное, «нематематическое» описание объекта или явления, которое предполагается моделировать. Затем это описание формулируется на языке математических формул. Это самый сложный этап построения модели. После этого создаются алгоритмы, по которым будут сделаны расчёты, затем производятся вычисления, а после полученные математические результаты интерпретируются, т. е. снова «переводятся» на обычный язык для того, чтобы понять, что именно получилось в результате работы математической модели. Если полученные результаты согласуются с реальностью, модель принимается за основу, а затем производится её доработка: в программу вводятся какие-то детали, не учтённые на первом этапе работы, или, наоборот, производятся некоторые упрощения, которые облегчают работу, но существенно не влияют на конечный результат.

Разумеется, модель всегда является упрощённым подобием реального объекта, так как какие-то детали всегда можно упустить из внимания или нарочно пренебречь для того, чтобы моделирование не оказалось чрезмерно сложным. Однако если основные особенности учтены и алгоритмы подобраны правильно, моделирование часто даёт поразительно точные результаты, позволяющие предсказывать ход природных процессов и рассчитывать работу сложных технических устройств. Бывает даже так, что в процессе моделирования выявляются результаты, неожиданные для её создателей, но абсолютно точно согласующиеся с реальностью.

В современном мире математическое моделирование находит широчайшее применение практически во всех областях человеческой деятельности – в электронной и космической технике, ядерной физике, экономике, социологии, экологии и сельском хозяйстве.

Рассмотрим широко известную в экологии модель, описывающую изменение численности двух видов, обитающих на данной территории: жертвы и хищника. Допустим, в определённой местности живут зайцы и лисы. Будем считать, что пища для зайцев имеется в избытке и поэтому они могут быстро размножаться в геометрической прогрессии. Следовательно, чем больше зайцев живёт в этом году, тем больше их родится в следующем. Так бы они и размножались бесконечно, если бы поблизости не обитали лисицы.

Эти хищники питаются зайцами и значительно сокращают их численность. Поэтому мы можем записать: зайцы + лисы → меньше зайцев.

Однако если зайцев окажется слишком мало, лисам станет нечего есть и они начнут вымирать от голода. Поэтому мы можем также написать другое уравнение: лисы – зайцы → меньше лис.

Попробуем решить систему этих уравнений, не прибегая к математическим вычислениям. Это будет называться качественным решением. Предположим, что в начальный момент у нас имеется некоторое число лис и достаточное число зайцев, чтобы лисы не ограничивали себя в питании. В этих условиях хищники начнут быстро размножаться и, когда их станет достаточно много, они станут съедать столько зайцев, что численность жертв начнёт убывать. Но по мере того как зайцев будет становиться всё меньше, лисам станет не хватать еды и они начнут вымирать от недостатка питания. Когда же их станет совсем мало, зайцы, оказавшиеся в относительной безопасности, снова начнут усиленно размножаться. Затем этот цикл повторится, и мы получим график, изображённый на рисунке (рис. 29). Он представляет собой две сдвинутые относительно друг друга колебательные линии, похожие на синусоиды.

Такая модель позволяет в известных пределах прогнозировать изменение численности обитающих на данной территории животных. Конечно, она, как любая модель, не свободна от упрощения и идеализации. Может, например, выдаться засушливое лето, и тогда наше предположение, что пища у зайцев всегда имеется в избытке, окажется неверным. В лес могут приехать охотники и сократить численность лис гораздо значительнее, чем это предполагает модель. В таком случае, если модель даёт неточные результаты, её, как было сказано, дорабатывают: вводят дополнительные факторы или исправляют алгоритмы. Любая модель, особенно в таких системах, где присутствует много случайных факторов, всегда должна быть динамичной и развивающейся.

Заканчивая разговор о математических моделях, обратим внимание ещё на одно интересное обстоятельство. Часто математические модели, разработанные для одного класса явлений, оказываются применимыми в совершенно другой области.

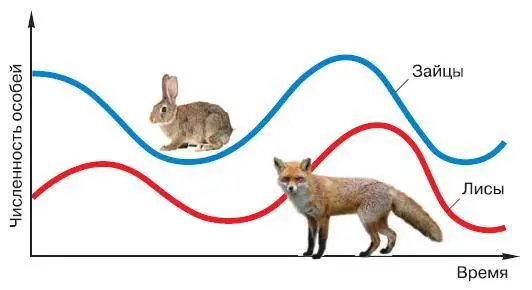
Рис. 29. Колебания численности популяций лисиц и зайцев

Те же математические уравнения, с помощью которых описывается взаимоотношение «хищник – жертва», с успехом используются при расчёте некоторых химических реакций. Это говорит об общности законов природы и присутствии в ней единых закономерностей.

1. Что называют моделью природного явления?

2. Перечислите этапы создания математической модели.

3. Что означает слово «алгоритм»? Приведите примеры алгоритмов, встречающихся в вашей повседневной жизни.

1. Нарисуйте график, где по оси абсцисс отложите число лисиц, а по оси ординат – число зайцев, обитающих в данном месте в данное время. Нарисуйте замкнутую кривую линию, которая будет характеризовать отношение этих чисел.

2. Возьмите два разных натуральных числа x и у, умножьте каждое на 2, произведения сложите и извлеките из суммы квадратный корень. Если корень окажется целым числом, значит x и у составляют полную пару. Найдите несколько пар, удовлетворяющих этому условию.