Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

© Соловьев А.В., перевод на русский язык, 2020

© Оформление. ООО «Издательство «Эксмо», 2021

Мой четырехлетний сын любит играть в саду. Его любимое занятие – выкапывать и рассматривать всяких ползучих тварей, особенно улиток. Если он достаточно терпелив, попавшие к нему в руки улитки, отойдя от первого шока, осторожно вылезают из своей раковины и начинают ползать по его маленьким ручкам, оставляя следы вязкой слизи. Когда же они ему наскучат, он равнодушно выбрасывает их в компостную кучу или на дрова за сараем.

В конце сентября прошлого года, после особенно напряженной охоты, откопав пять или шесть больших особей и избавившись от них, он подошел ко мне, когда я пилил дрова для костра, и спросил: «Папа, а сколько там, в саду, улиток?» Обманчиво простой вопрос, на который у меня не было хорошего ответа. Их могла быть сотня или тысяча. Честно говоря, разницы он бы не понял. Тем не менее его вопрос вызвал у меня интерес. С этим определенно стоило разобраться вместе.

Мы решили провести эксперимент. Ближайшим субботним утром мы пошли собирать брюхоногих. Через десять минут у нас оказалось в общей сложности 23 улитки. Я вытащил из заднего кармана маркер и пометил каждую крестиком. Как только они все были помечены, мы опорожнили ведро, выпустив улиток обратно в сад.

Через неделю мы совершили новый заход. На этот раз за десять минут мы добыли лишь 18 улиток. Осмотрев их внимательно, мы обнаружили у трех из них на раковинах крестик; у оставшихся 15 его не было. Вот и все, что нам требовалось для подсчета.

Идея заключается в следующем: количество улиток, которых мы поймали в первый день (23) – это некоторая часть общей численности брюхоногого населения сада, «перепись» которого мы хотим провести. Если мы вычислим, какую долю она составляет, то сможем найти размер всей популяции. Поэтому мы используем вторую выборку (тех, что наловили в следующую субботу). Число отмеченных особей в ней (3 из 18) должно составлять ту же долю, что и общее число отмеченных от всех особей в саду. Упростив это соотношение, мы обнаружим, что пометили каждую шестую особь (как вы можете видеть на рис. 1). Далее, умножив число помеченных в первый день особей (23) на 6, мы получим общее число улиток в саду – 138.

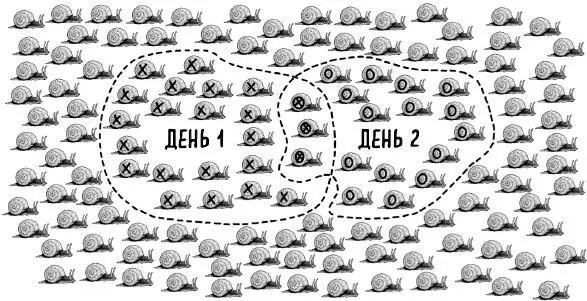
Рис. 1. Отношение количества повторно пойманных улиток (ОХ) к общему количеству пойманных во второй день (О) должно быть таким же, как и отношение количества пойманных в первый день (Х) к общему количеству улиток в саду, помеченных и не помеченных – 3:18 и 23:138 соответственно

После завершения этого мысленного расчета я обратился к своему сыну, который «присматривал» за собранными нами улитками. Как он прокомментировал мое заявление, что в саду обитает примерно 138 улиток? «Папа, – сказал он, не отводя глаз от осколков раковины, все еще липнущих к его пальцам, – я убил ее». Ну, тогда 137.

Этот простой математический метод, известный как мечение и повторный отлов, был разработан экологами для оценки размеров популяций животных. Вы можете использовать его самостоятельно, взяв два независимых образца и сравнив пересечения этих множеств. Так можно оценить количество лотерейных билетов, проданных на местной ярмарке, или посещаемость футбольного матча, не затрудняясь утомительным подсчетом по головам, а оперируя корешками билетов.

Метод мечения и повторного отлова используется и в серьезных научных проектах. Он может дать, например, жизненно важную информацию о колебаниях численности вида, находящегося под угрозой исчезновения. Оценка количества рыбы в водоеме [1] Pollock, K. H. (1991). Modeling capture, recapture, and removal statistics for estimation of demographic parameters for fish and wildlife populations: past, present, and future. Journal of the American Statistical Association, 86 (413), 225. https://doi.org/10.2307/2289733 поможет рыбхозяйству определить, сколько можно выдать разрешений на рыбалку. Этот метод настолько эффективен, что его применение вышло за рамки экологии и позволяет узнать размер любых групп – от количества наркоманов среди населения [2] Doscher, M. L., & Woodward, J. A. (1983). Estimating the size of subpopulations of heroin users: applications of log-linear models to capture/recapture sampling. The International Journal of the Addictions, 18 (2), 167–82. Hartnoll, R., Mitcheson, M., Lewis, R., & Bryer, S. (1985). Estimating the prevalence of opioid dependence. Lancet, 325 (8422), 203–5. https://doi.org/10.1016/S0140-6736 (85) 92036–7 Woodward, J. A., Retka, R. L., & Ng, L. (1984). Construct validity of heroin abuse estimators. International Journal of the Addictions, 19 (1), 93–117. https://doi.org/10.3109/10826088409055819 до числа погибших во время войны в Косово [3] Spagat, M. (2012). Estimating the Human Costs of War: The Sample Survey Approach. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780195392777.013.0014 . Такова практическая сила простых математических идей. Именно такие концепции мы разберем в этой книге, и именно их я регулярно использую в своей повседневной работе – математической биологии.

Когда я говорю людям, что занимаюсь математической биологией, в ответ мне обычно вежливо кивают, и этот кивок сопровождается неловким молчанием – будто я собираюсь проверить, помнят ли они теорему Пифагора или как решать квадратное уравнение. Люди не просто теряются – им сложно понять, какое отношение математика, которую они воспринимают как абстрактный, чисто теоретический и отвлеченный предмет, может иметь к биологии, которая, как правило, считается предметом практичным, «приземленным» и прикладным. С такой искусственной дихотомией, люди часто впервые сталкиваются еще в школе: если вам нравились естественнонаучные дисциплины, но алгебра особо не давалась, вас «спихивали» изучать биологию. Если вам, как и мне, нравились естественные науки, но вас (как и меня) не прельщала идея потрошить мертвые тушки (в начале курса по препарированию я как-то раз упал в обморок, когда зашел в лабораторию и увидел на своем рабочем месте рыбью голову), то вам приходилось идти на физику. Вместе им не сойтись…

Так было и со мной. В старших классах я бросил биологию и сдавал экзамены для поступления в институт по математике (основной и углубленный курс), физике и химии. В университете мне пришлось еще больше упорядочить свой учебный план. Меня расстраивало, что придется навсегда оставить биологию: предмет, который, как мне казалось, обладал невероятной силой, способной изменить жизнь к лучшему. Я с нетерпением предвкушал возможностью окунуться в мир математики, но опасался, что берусь за предмет, малоприменимый на практике. Сильнее ошибиться я не мог.

Я грыз гранит «голой» математики, которой нас учили в университете, запоминал доказательство теоремы о промежуточном значении или определение векторного пространства, но настоящим смыслом жизни для меня стали курсы прикладной математики.