Мелани Митчелл - Идиот или гений? Как работает и на что способен искусственный интеллект

Рис. 1. A: нейрон в мозге; В: простой перцептон

Иными словами, перцептрон – это простая программа, которая принимает решение “да или нет” (1 или 0) в зависимости от того, достигает ли сумма взвешенных входных сигналов порогового значения. Вероятно, вы тоже время от времени принимаете такие решения в жизни. Например, вы узнаете мнение нескольких друзей о конкретном фильме, но вкусам одних друзей доверяете больше, чем вкусам других. Если сумма “дружеских восторгов” – при большем весе мнений тех друзей, которым вы доверяете больше, – достаточно высока (то есть превышает некоторый неосознанный порог), вы решаете посмотреть фильм. Именно так перцептрон выбирал бы фильмы к просмотру, если бы у него были друзья.

Вдохновленный сетями нейронов в мозге, Розенблатт предположил, что сети перцептронов могут выполнять визуальные задачи, например справляться с распознаванием объектов и лиц. Чтобы понять, как это может работать, давайте изучим, как с помощью перцептрона решить конкретную визуальную задачу: распознать рукописные цифры вроде тех, что показаны на рис. 2.

Давайте сделаем перцептрон детектором восьмерок – в таком случае он будет выдавать единицу, если входным сигналом служит изображение цифры 8, и ноль, если на входном изображении будет любая другая цифра. Чтобы создать такой детектор, нам нужно (1) понять, как превратить изображение в набор численных входных сигналов, и (2) определить численные значения весов и порог перцептрона для формирования верного выходного сигнала (1 для восьмерок и 0 для других цифр). Я рассмотрю эту задачу более подробно, поскольку многие из этих принципов понадобятся нам при обсуждении нейронных сетей и их применения в компьютерном зрении.

Рис. 2. Примеры рукописных цифр

На рис. 3A показана увеличенная рукописная восьмерка. Каждый квадрат координатной сетки – это пиксель с численным значением “насыщенности”: насыщенность белых квадратов равняется 0, насыщенность черных – 1, а насыщенность серых имеет промежуточное значение. Допустим, все изображения, которые мы даем перцептрону, подогнаны к единому размеру – 18 × 18 пикселей. На рис. 3B показан перцептрон для распознавания восьмерок. У этого перцептрона 324 (то есть 18 × 18) входных сигнала, каждый из которых соответствует одному пикселю из сетки 18 ×18. При получении изображения, подобного показанному на рисунке 3A, каждый входной сигнал настраивается на насыщенность соответствующего пикселя. Каждому входному сигналу также присваивается свой вес (на рисунке не показан).

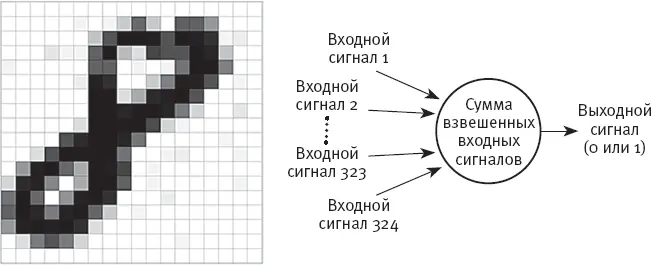
Рис. 3. Иллюстрация перцептрона, который распознает рукописные восьмерки. Каждый пиксель на изображении 18 × 18 пикселей соответствует одному входному сигналу перцептрона, что дает 324 (= 18 × 18) входных сигнала.

В отличие от символической системы Универсального решателя задач, которую я описала ранее, перцептрон не имеет очевидных правил для выполнения задачи, а все его “знания” закодированы в числах, определяющих веса входных сигналов и пороговое значение. В ряде статей Розенблатт показал, что при корректных весах и пороговом значении такой перцептрон, как на рисунке 3B, вполне неплохо справляется с такими задачами на восприятие, как распознавание простых рукописных цифр. Но как именно определить корректные веса и пороговое значение для конкретной задачи? И снова Розенблатт предложил ответ, навеянный работой мозга: перцептрон должен сам узнавать эти значения. Но каким образом? Вторя популярным в то время теориям бихевиоральной психологии, Розенблатт считал, что перцептроны должны обучаться, накапливая условный рефлекс . Отчасти вдохновленный работой бихевиориста Б. Ф. Скиннера, который обучал крыс и голубей выполнять задачи с помощью положительного и отрицательного подкрепления, Розенблатт полагал, что перцептрон следует обучать на примерах: его нужно вознаграждать, когда он выдает верный результат, и наказывать, когда он ошибается. Теперь такая форма обучения в ИИ называется обучением с учителем. В ходе обучения система получает пример и генерирует выходной сигнал, а затем получает “сигнал от учителя”, который показывает, насколько выходной сигнал системы отличается от верного. Затем система использует этот сигнал, чтобы скорректировать веса и пороговое значение.

Концепция обучения с учителем – ключевой элемент современного ИИ, поэтому ее стоит разобрать подробнее. Как правило, обучение с учителем требует большого набора положительных (скажем, коллекции восьмерок, написанных разными людьми) и отрицательных (скажем, коллекции других рукописных цифр, среди которых нет восьмерок) примеров. Каждый пример размечается человеком, который присваивает ему определенную категорию (метку) – здесь это “восьмерка” и “не восьмерка”. Метка применяется в качестве контрольного сигнала. Некоторые положительные и отрицательные примеры используются для тренировки системы и формируют тренировочное множество . Оставшиеся примеры – тестовое множество – используются для оценки работы системы после обучения, чтобы понять, насколько хорошо она научилась правильно отвечать на запросы в целом, а не только на обучающие примеры.

Вероятно, самым важным в информатике стоит признать понятие “алгоритм”. Оно обозначает “рецепт” со списком шагов, которые компьютер может предпринять для решения конкретной задачи. Главным вкладом Фрэнка Розенблатта в ИИ стало создание особого алгоритма, названного алгоритмом обучения перцептрона. С помощью этого алгоритма перцептрон можно научить на примерах определять веса и пороговое значение для получения верных ответов. Вот как он работает: сначала весам и порогу присваиваются случайные значения в диапазоне от –1 до 1. В нашем примере первому входному сигналу может быть присвоен вес 0,2, второму – вес –0,6 и так далее. Пороговым значением может стать 0,7. С генерацией начальных значений без труда справится компьютерная программа, называемая генератором случайных чисел.

Теперь мы можем приступать к процессу обучения. Перцептрон получает первый обучающий пример, не видя метку с верной категорией. Перцептрон умножает каждый входной сигнал на его вес, суммирует результаты, сравнивает сумму с пороговым значением и выдает либо 1, либо 0. Здесь выходной сигнал 1 означает, что перцептрон распознал восьмерку, а выходной сигнал 0 – что он распознал “не восьмерку”. Далее в процессе обучения выходной сигнал перцептрона сравнивается с верным ответом, который дает присвоенная человеком метка (“восьмерка” или “не восьмерка”). Если перцептрон прав, веса и пороговое значение не меняются. Если же перцептрон ошибся, веса и пороговое значение слегка корректируются так, чтобы сумма входных сигналов в этом тренировочном примере оказалась ближе к нужной для верного ответа. Более того, степень изменения каждого веса зависит от соответствующего значения входного сигнала, то есть вина за ошибку в основном возлагается на входные сигналы, которые сильнее других повлияли на результат. Например, в восьмерке на рис. 3A главным образом на результат повлияли бы более насыщенные (здесь – черные) пиксели, в то время как пиксели с нулевой насыщенностью (здесь – белые) не оказали бы на него никакого влияния. (Для любопытных читателей я описала некоторые математические подробности в примечании [30] Математически алгоритм обучения перцептрона описывается следующим образом. Для каждого веса w j : w j ← w j + η ( t – y ) x j , где t – верный выходной сигнал (1 или 0) для заданного входного сигнала, y – фактический выходной сигнал перцептрона, x j – входной сигнал, связанный с весом w j , а η – скорость обучения , задаваемая программистом. Стрелка обозначает обновление. Порог учитывается путем создания дополнительного “входного сигнала” x 0 с постоянным значением 1, которому присваивается вес w 0 = – порог . При наличии этого дополнительного входного сигнала и веса (называемого смещением) перцептрон дает сигнал на выходе, только если сумма входных сигналов, помноженных на веса (то есть скалярное произведение входного вектора и вектора веса) больше или равняется 0. Часто входные значения масштабируются и подвергаются другим преобразованиям, чтобы веса не становились слишком велики. .)