Анатолий Молчанов - В поисках общей теории роста человечества

«В 1960 году в журнале «Science» была опубликована статья трех авторов Х. Фостера, П. Мориа и Л. Эмиота, которая называлась «День страшного суда пятница 13 ноября 2026 года». Используя тщательно отобранные статистические данные авторы показали, что относительный прирост населения растет так же быстро, как само население. Чем объясняется такая зависимость, остается пока неясным». «…»

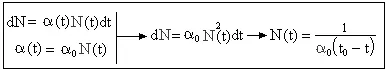
Рис. 2. Пропорциональность коэффициента мирового естественного прироста общей численности народонаселения позволяет объяснить гиперболический рост населения Земли.

«…Сокращение смертности в целом по земному шару перекрывает уменьшение рождаемости в отдельных (особенно развитых странах), так что естественный прирост на Земле возрастает со временем. Менее ясно почему он растет столь же стремительно как само население, что собственно и приводит к гиперболическому закону. Это пока остается загадкой» [22], стр. 471.

Здесь Л.М. Гиндилис допускает две серьезные ошибки. Первая заключается в том, что, отождествляя закон гиперболического роста численности населения мира с причинным степенным законом квадратичного роста (который утверждает, что причина гиперболического роста заключается в ПОС второго порядка между скоростью роста и численностью), он приписывает Фёрстеру открытие, которого тот не совершал.

Исследование Фёрстера и его коллег касается только зависимости численности от времени, которая была получена при обработке большого количества данных по методу наименьших квадратов. Как в точности, если не говорить о средних величинах, зависела при этом скорость роста численности от численности и от времени, и как зависел коэффициент прироста от численности – остается неизвестным.

На самом деле эмпирическая зависимость численности от времени, открытая Фёрстером и его коллегами, могла быть получена и при другом, отличном от закона квадратичного роста, дифференциальном причинном законе роста. Неясно даже может ли вообще гиперболический рост населения мира, учитывая непонятную, парадоксальную системность человечества, без которой он никогда бы не проявился, быть объяснен с помощью законов с простой преддетерминацией. Связь между скоростью роста и численностью в таком случае в период гиперболического роста могла и не быть причинно-следственной.

Вторая ошибка вполне логична и заключается в том, что автор подменяет здесь проблему гиперболического роста численности населения Земли на проблему линейной зависимости коэффициента мирового естественного прироста от численности.

Если коэффициент естественного прироста для каждого села, города, страны, региона – един и пропорционален численности населения мира: α = α oN, то сложив эти приросты (dN i= α oN*N i) по всему земному шару, и вынеся α oN за скобку, получим закон квадратичного роста dN/dt = α oN(N 1+…+ N n) = α oN 2, а проинтегрировав его – гиперболу Фёрстера.

Таким образом, Л.М. Гиндилис одним махом решает все проблемы, связанные с аномальной системностью человечества, над которыми безуспешно бьются все исследователи гиперболического роста. Беда здесь только в том, что такая зависимость коэффициента глобального естественного прироста от численности представляется совершенно невозможной по следующей причине:

В таком случае приходится постулировать единый и синхронно растущий по закону простой пропорции коэффициент прироста для населения всех стран и народов, когда-либо населявших Землю, т. е. растущий пропорционально не численности каждого такого выделенного народа или страны, а мира в целом, что представляется совершенно немыслимым.

Следовательно, вопрос здесь не в том, почему относительный глобальный естественный прирост пропорционален численности населения мира. Это неправильно поставленный вопрос. Само представление о том, что гиперболический рост населения Земли может быть объяснен с помощью причинного степенного закона квадратичного роста является ошибочным.

Рост популяции, выраженный степенным или каким-либо другим нелинейным законом, не может быть полностью описан лишь с помощью самого этого закона, т. к. такой закон сам по себе не может объяснить информационную связность растущей популяции, взаимозависимость роста всех ее частей.

Кроме того, рост популяции, происходящий по степенному закону, имеет и свои, специфические, присущие только ему особенности, не позволяющие принять этот закон в качестве причинного закона для описания роста какой-либо реально существовавшей в природе популяции. Перечислим все эти аномальные особенности параболического и гиперболического роста:

1. Оба они имеют особую, выделенную на оси времени точку: момент начала или завершения роста, численность популяции в которой равна нулю для параболического и бесконечности для гиперболического роста. Поскольку такое в реальности невозможно, да и само наличие таких особых точек на шкале роста должно иметь какое-то объяснение, следует признать, что непрерывная модель степенного роста как процесса с простой преддетерминацией изначально содержит в себе внутренние противоречия.

2. Хотя численность популяции при степенном, так же как и при экспоненциальном росте изменяется по закону геометрической прогрессии, но рост этот происходит на последовательности интервалов времени расширяющихся (параболический рост) или сжимающихся (гиперболический рост) по закону прогрессии от/к особой точки/е этого роста.

Это увеличение (уменьшение) времени удвоения численности популяции выполняется при отсчете времени (прямом или обратном) только от этой точки и ни от какой другой, что еще раз подчеркивает ее выделенность. Такой рост, в отличие от экспоненциального роста, является существенно неоднородным во времени процессом. Если взять два равных отрезка времени, различающихся своим положением на шкале роста, то рост численности, в том числе и размножение каждой единичной особи популяции, будет происходить на них совершенно по разному.

Рассмотрим, например, простой гиперболический рост на последовательности отрезков времени, сокращающихся по закону прогрессии со знаменателем 1/2 (так росло население Земли). На каждом таком отрезке время удвоения численности уменьшается вдвое по сравнению с предыдущим, что говорит о том, что особи популяции будут здесь более плодовитыми и/или потери от смертности меньшими [93] Плодовитость может расти, смертность падать, но почему закон, по которому это происходит, именно такой, какой он есть и почему этот закон остается неизменным в течение длительного промежутка времени? .