Шон Кэрролл - Квантовые миры и возникновение пространства-времени

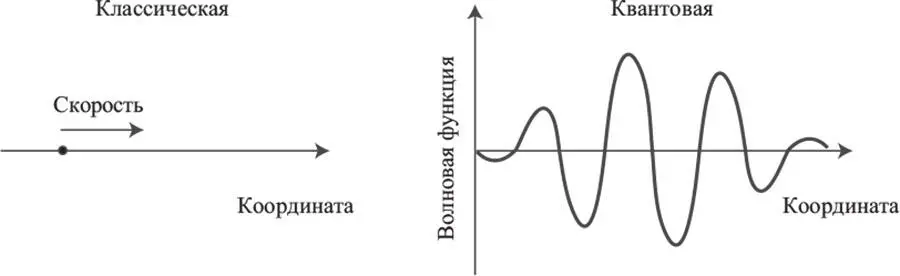
Такое облако часто называют волновой функцией , поскольку оно может колебаться подобно волне, по мере того как со временем изменяется наиболее вероятный результат измерения. Волновая функция обычно обозначается греческой буквой «пси» (Ψ). Для каждого возможного результата измерения, например координаты частицы, волновая функция позволяет присвоить конкретное число, называемое амплитудой , связанной с данным результатом. Так, амплитуда, с которой частица может оказаться в конкретной точке x 0, будет записываться как Ψ( x 0).

Вероятность получить такой результат при измерениях равна квадрату амплитуды.

Вероятность конкретного результата = |Амплитуда данного результата| 2

Это простое отношение называется правилом Борна в честь физика Макса Борна [2] Есть одна небольшая техническая деталь, которую хотелось бы здесь упомянуть; затем смело забудем о ней. Амплитуда любого конкретного результата фактически является комплексным, а не вещественным числом. Вещественные числа входят в ряд всех чисел, расположенных между минус бесконечностью и бесконечностью. Возводя в квадрат вещественное число, мы всякий раз получаем другое вещественное число, которое больше или равно нулю. Поэтому если говорить строго о вещественных числах, то квадратного корня из отрицательного числа просто не существует. Математики давным-давно осознали, что квадратные корни из отрицательных чисел были бы очень удобны, поэтому и ввели такое понятие, как мнимая единица – комплексное число, являющееся квадратным корнем из –1. Мнимое число – это просто вещественное число, называемое мнимой частью, умноженное на i . В таком случае комплексное число состоит из двух частей: вещественной и мнимой. Вертикальные черточки у члена |Амплитуда| 2 в формуле правила Борна означают, что мы фактически складываем квадраты вещественной и мнимой частей. Все это я написал только для самых въедливых читателей: далее я буду говорить просто «вероятность – это амплитуда в квадрате» и этим удовлетворюсь. . Часть стоящей перед нами задачи – разобраться, откуда в мире взялось такое правило.

Совершенно определенно следующее: мы не утверждаем, что есть электрон, обладающий некоторой координатой и скоростью; мы попросту не знаем этих значений, и эта наша неосведомленность как раз заключена в волновой функции. В этой главе мы ничего не говорим о том, что «есть», а отмечаем лишь то, что мы наблюдаем. В следующих главах я вообще стану упирать на то, что волновая функция – это и есть истинная сумма свойств реальности, а такие идеи, как скорость и координата электрона, – всего лишь характеристики, которые мы в силах измерить. Но не все разделяют эту точку зрения, поэтому пока постараемся сохранять беспристрастность.

Давайте сопоставим правила классической и квантовой механики и сравним их. Состояние классической системы описывается координатами и скоростью всех движущихся в ней элементов. Чтобы проследить ее эволюцию, представим себе примерно следующую процедуру:

Правила классической механики

1. Подготавливаем систему, фиксируя конкретные координаты и скорость для каждой из ее частей.

2. Следим за эволюцией системы в соответствии с ньютоновскими законами движения.

Вот и все. Дьявол, естественно, в деталях. В некоторых классических системах движущихся элементов очень много.

В свою очередь, в типичном учебнике по квантовой механике описание правил дается в двух частях. В первой части имеем структуру, строго эквивалентную той, что представлена в классическом случае. Квантовые системы описываются волновыми функциями, а не координатами и скоростями. Точно как в классической механике ньютоновские законы движения управляют эволюцией состояния системы, в квантовой системе есть уравнение, описывающее, как эволюционирует волновая функция. Оно называется уравнением Шрёдингера. Уравнение Шрёдингера можно сформулировать так: «Скорость изменения волновой функции пропорциональна энергии квантовой системы». Чуть более строгая формулировка такова: волновая функция может описывать состояния с различными энергиями, и, согласно уравнению Шрёдингера, высокоэнергетические части волновой функции эволюционируют стремительно, а низкоэнергетические – очень медленно. Что, если подумать, вполне логично.

Для наших целей важно лишь то, что существует уравнение, позволяющее спрогнозировать, как волновые функции гладко [3] Здесь и далее в книге под гладкостью эволюции волновой функции подразумевается ее непрерывное и плавное изменение с течением времени, без скачков или коллапса. – Примеч. науч. ред. эволюционируют с течением времени. Эта эволюция столь же неизбежна и предсказуема, как и движение тел в соответствии с законами Ньютона в классической механике. Пока – ничего экстраординарного.

Правила квантовой механики (часть первая)

1. Подготавливаем систему, фиксируя конкретную волновую функцию Ψ.

2. Далее система эволюционирует согласно уравнению Шрёдингера.

Пока все нормально – эти элементы квантовой механики строго соотносятся с их классическими предшественниками. Вот только правила классической механики на этом заканчиваются, а в игру вступают дополнительные правила квантовой.

Все эти дополнительные правила связаны с измерением. Измеряя, например, спин или координату частицы, мы, согласно квантовой механике, в любом случае получим лишь определенные, возможные в данном случае результаты. Конкретный результат спрогнозировать не выйдет, но можно рассчитать вероятность получения каждого из возможных результатов. После того как измерение будет выполнено, волновая функция коллапсирует , превращаясь в совершенно новую функцию, в которой все вероятности сконцентрированы вокруг именно того результата, который вы только что получили. Таким образом, измеряя квантовую систему, максимум, на что вы можете рассчитывать – это возможность спрогнозировать вероятность различных ее результатов. Но если вы сразу повторите измерение той же самой величины, то раз за разом будете получать один и тот же результат – волновая функция сколлапсировала в него.

И вот самый сок нашего разбора.

Правила квантовой механики (часть вторая)

3. Существуют определенные наблюдаемые величины, которые по желанию можно измерить, – например координата частицы. По итогам измерения ее координаты мы получим вполне определенный результат.

4. Вероятность получения любого конкретного результата вычисляется исходя из волновой функции. Волновая функция связывает амплитуду с каждым из возможных результатов измерения; вероятность любого результата есть квадрат амплитуды волновой функции.