Адам Кучарски - Законы эпидемий. Как развиваются и почему прекращаются эпидемии болезней, финансовые кризисы, вспышки насилия и модные тренды

Летним вечером 1924 года во время эксперимента, который проводил Уильям Кермак, произошел взрыв, и едкая щелочь попала ему в глаза. Химик по образованию, Кермак изучал методы анализа спинномозговой жидкости. В тот вечер в лаборатории Королевского колледжа Эдинбурга он работал один. Ему пришлось два месяца провести в больнице, и после этого несчастного случая 26-летний Кермак полностью ослеп [41] Биографические данные Кермака взяты из Davidson J.N., ‘William Ogilvy Kermack’, Biographical Memoirs of Fellows of the Royal Society, 1971; Coutinho S.C., ‘A lost chapter in the pre-history of algebraic analysis: Whittaker on contact transformations’, Archive for History of Exact Sciences, 2010. .

Во время пребывания в больнице Кермак просил друзей и сиделок читать ему книги по математике. Понимая, что зрение к нему не вернется, он тренировался получать информацию другим путем. У него была превосходная память, и математические задачи он решал в уме. «Просто невероятно, как много он мог сделать, не имея возможности записать что-либо на бумаге», – восхищался его коллега Уильям Маккри.

Выписавшись из больницы, Кермак продолжил заниматься наукой, но переключился на другие области. Он оставил химические опыты и начал разрабатывать новые проекты. В частности, он работал над математическим обеспечением исследований вместе с Андерсоном Маккендриком, который возглавил лабораторию в Эдинбурге. Проработав в Индийской медицинской службе два десятка лет, в 1920 году Маккендрик уволился и вместе с семьей переехал в Шотландию.

Кермак и Маккендрик развивали идеи Росса, пытаясь применить их к эпидемиям в целом. Они сосредоточились на одном из главных вопросов в изучении болезней: что приводит к окончанию эпидемии? В то время существовало два популярных объяснения. Либо передача инфекции прекращалась потому, что не оставалось восприимчивых к ней людей, либо по мере распространения эпидемии патоген становился менее заразным. Как выяснилось, в большинстве случаев оба объяснения неверны [42] Kermack W.O. and McKendrick A.G., ‘A Contribution to the Mathematical Theory of Epidemics’, Proceedings of the Royal Society A, 1927. .

Как и Росс, Кермак и Маккендрик начали с разработки математической модели передачи болезни. Для простоты они предположили, что население перемешивается случайным образом. Подобно тому как это происходит при встряхивании камешков в сосуде, каждый человек в популяции обладает равными шансами встретиться с любым другим. В их модели эпидемия начиналась с определенного количества больных людей, а все остальные были восприимчивы к инфекции. После выздоровления человек приобретал иммунитет. Таким образом, всех людей в популяции можно разделить на три группы на основе их состояния:

Эту модель часто называют «моделью SIR » – по первым буквам названий групп ( англ. susceptible, infectious, recovered ). Предположим, в популяции численностью 10 тысяч человек один человек заболевает гриппом. Если мы смоделируем эпидемию гриппа с помощью модели SIR , то получим следующую кривую:

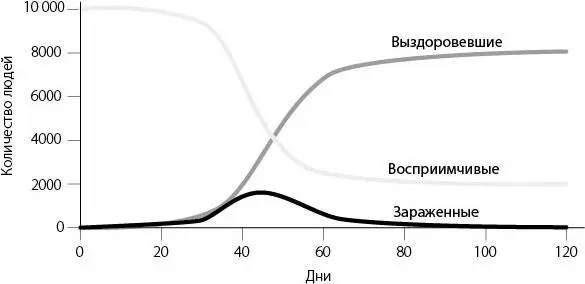
Модель SIR для эпидемии гриппа

Смоделированная здесь эпидемия развивается медленно, поскольку начинается с одного зараженного человека, но через 50 дней все равно достигает пика. Через 80 дней она практически заканчивается. Обратите внимание, что в конце эпидемии по-прежнему остается какое-то количество восприимчивых людей. Если бы заразились все 10 тысяч человек, то все они в конце концов попали бы в группу «Выздоровевшие». Модель Кермака и Маккендрика указывает на то, что этого не случится: вспышка заболевания может закончиться прежде, чем переболеют все до единого. «В общем случае эпидемия заканчивается раньше, чем заканчивается восприимчивое население», – писали они.

Почему заражаются не все? Все дело в переломе, который происходит в середине вспышки. На ранних этапах эпидемии восприимчивых людей много. В результате каждый день число новых зараженных превышает число выздоровевших, и эпидемия набирает обороты. Но со временем количество восприимчивых людей сокращается. Когда их становится достаточно мало, тенденция обращается вспять: ежедневно число выздоровевших превышает число зараженных, и эпидемия идет на спад. Еще остаются восприимчивые к инфекции люди, которые могут заразиться, но их немного, и у любого заболевшего больше шансов выздороветь, чем заразить кого-то еще.

Для иллюстрации этого эффекта Кермак и Маккендрик показали, как модель SIR воспроизводит динамику эпидемии чумы в Бомбее (ныне Мумбаи). В модели заразность патогена не меняется со временем; развитие и спад эпидемии зависят от меняющегося числа восприимчивых и зараженных.

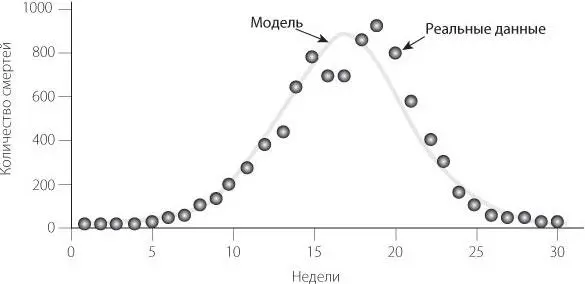
Эпидемия чумы в Бомбее в 1906 году: модель и реальные данные

Перелом наступает на пике эпидемии. В этот момент людей с иммунитетом становится так много, а восприимчивых так мало, что эпидемия больше не может разрастаться. Поэтому тенденция меняется на противоположную, и начинается спад.

Когда в популяции набирается достаточное количество людей с иммунитетом, чтобы передача инфекции прекратилась, мы говорим о появлении стадного (коллективного) иммунитета. Этот термин предложил в начале ХХ века статистик Мейджор Гринвуд [43] Fine P.E.M., ‘Herd Immunity: History, Theory, Practice’, Epidemiologic Reviews, 1993; Farewell V. and Johnson T., ‘Major Greenwood (1880–1949): a biographical and bibliographical study’, Statistics in Medicine, 2015. . Ранее психологи уже использовали термин «стадный инстинкт», описывая поведение групп, члены которых действуют коллективно, а не как отдельные личности [44] Dudley S.F., ‘Herds and Individuals’, Public Health, 1928. . Аналогичным образом, наличие стадного иммунитета означает, что население в целом способно блокировать передачу инфекции несмотря на то, что отдельные люди остаются восприимчивыми к ней.

Концепция коллективного иммунитета обрела популярность несколько десятилетий спустя, когда стало ясно, что это мощное средство борьбы с болезнями. Во время эпидемии люди перестают быть восприимчивыми к инфекции естественным образом – по мере заражения. Но в случае со многими болезнями органы здравоохранения могут целенаправленно, путем вакцинации, выводить людей из группы восприимчивых. В свое время Росс предположил, что малярию можно победить, не уничтожая всех комаров; точно так же коллективный иммунитет позволяет остановить распространение инфекции без необходимости вакцинировать все население. Есть категории людей, которых нельзя вакцинировать: это, например, новорожденные младенцы и люди с ослабленной иммунной системой, – но благодаря коллективному иммунитету привитые люди защищают не только себя, но и эти уязвимые группы [45] Hendrix K.S. et al., ‘Ethics and Childhood Vaccination Policy in the United States’, American Journal of Public Health, 2016. . А если болезнь можно контролировать с помощью вакцинации, значит, теоретически от нее можно избавиться навсегда. Вот почему концепция коллективного иммунитета занимает центральное место в теории эпидемий. «У этой концепции особая аура», – так однажды выразился эпидемиолог Пол Файн [46] Fine P.E.M., ‘Herd Immunity: History, Theory, Practice’, Epidemiologic Reviews, 1993. .