Youri Kraskov - The Wonders of Arithmetic from Pierre Simon de Fermat

2=(Y–Q)

A 1= B 1, where A 11

Now we get a situation similar to the one with numbers A, B only with smaller numbers A 1, B 1. Analyzing now (5) in the manner described above we will be forced to admit that there must exist numbers

A 2=B 2, where A 2

Following this path, we will inevitably come to the case when the existence of numbers A k=B k, where A kk-1; B kk-1as a direct consequence of assumption (1) will become impossible. Therefore, our initial assumption (1) is also impossible and thus the theorem is proven. 41

Looking at this very simple and even elementary proof by the descent method naturally a puzzling question arise, how could it happen that for many centuries science not only had not received this proof, but was completely ignorant that it had not any one in general? On the other hand, even being mistaken in this matter i.e. assuming that this theorem was proven by Euclid, how could science ignore it by using the "complex numbers" and thereby dooming itself to destruction from within? And finally, how can one explain that this very simple in essence theorem, on which the all science holds, is not taught at all in a secondary school?

As for the descent method, this proof is one of the simplest examples of its application, which is quite rare due to the wide universality of this method. More often, the application of the descent method requires a great strain of thought to bring a logical chain of reasoning under it. From this point of view, some other special examples of solving problems by this method can be instructive.

We will now consider another example of the problem from Fermat's letter-testament, which is formulated there as follows:

There is only one integer square, which increased by two, gives a cube, this square is 25 .

When at the suggestion of Fermat, the best English mathematician of the time John Wallis tried to solve it, he was very vexed and forced to acknowledge he could not do it. For more than two centuries it was believed that Leonard Euler received the solution to this problem, but his proof is based on the use of "complex numbers", while we know these are not numbers at all because they do not obey the Basic theorem of arithmetic. And only at the end of the twentieth century André Weil using the Fermat's triangles method still managed to get a proof [17].

It was a big progress because a purely arithmetic method was used here, however, as applied to this problem, it was clearly dragged the ears. Could Fermat solve this problem easier? We will also extract the answer to this question from the cache, what will allow us to reveal this secret of science in the form of the following reconstruction. So, we have the equation p 3=q 2+2 with the obvious solution p=3, q=5. To prove Fermat's assertion, we suppose that there is another solution P>p=3, Q>q=5, which satisfies the equation

P 3=Q 2+2 (1)

Since it is obvious that Q>P then let Q=P+δ (2)

Substituting (2) in (1) we obtain: P 2(P–1)–2δP–δ 2=2 (3)

Here we need just a little bit of “sharpness of mind” to notice that δ>P otherwise equation (3) is impossible. Indeed, if we make a try δ=P then on the left (3) there will be P 2(P–4)>2 what is not suitable, therefore there must exist a number δ 1=δ–P. Then substituting δ=P+δ 1in (3) we obtain

P 2(P–4)–4δ 1P–δ 1 2=2 (4)

Now we will certainly notice that δ 1>P otherwise, by the same logic as above, on the left (4) we get P 2(P–9)>2 what again does not suitable, then there must exist a number δ 2=δ 1–P and after substituting δ 1=P+δ 2in (4), we obtain P 2(P–9)–6δ 2P–δ 2 2=2 (5)

Here one can no longer doubt that this will continue without end. Indeed, by trying δ i=P each time we get P 2(P−K i)>2. Whatever the number of K ithis equation is impossible because if K i

3 then P 2(P−K i)>2 and if K i≥P then this option is excluded because then P 2(P−K i)≤0

To continue so infinitely is clearly pointless, therefore our initial assumption of the existence of another solutions P>3, Q>5 is false and this Fermat's theorem is proven.

In the book of Singh, which we often mention, this task is given as an example of the “puzzles” that Fermat was “inventing”. But now it turns out that the universal descent method and a simple technique with trying, make this task one of the very effective examples for learning at school.

Along with this proof, students can easily prove yet another theorem from Fermat’s letter-testament, which could be solved only by such a world-famous scientist as Leonard Euler:

There are only two squares that increased by 4, give cubes, these squares will be 4 and 121.

In other words, the equation p 3=q 2+4 has only two integer solutions.

We remind that in the Fermat's letter-testament only a special case of this theorem for squares is stated. But also, this simplified version of the task was beyond the power not only of representatives of the highest aristocracy Bachet and Descartes, but even the royal-imperial mathematician Euler.

However, another royal mathematician Lagrange, thanks to the identity found by Euler, still managed to cope with the squares and his proof of only one particular case of FGT is still replicated in almost all textbooks. However, there is no reasonable explanation that the general proof of the FGT for all polygonal numbers obtained by Cauchy in 1815 was simply ignored by the scientific community.

We begin our study with the formulation of the FGT from Fermat's letter to Mersenne in 1636. It is presented there as follows:

Every number is equal

one, two or three triangles,

one, 2, 3 or 4 squares,

one, 2, 3, 4 or 5 pentagons,

one, 2, 3, 4, 5 or 6 hexagons,

one, 2, 3, 4, 5, 6 or 7 heptagons,

and so on to infinity [36].

Since polygonal numbers are clearly not respected by today's science, we will give here all the necessary explanations. The formula for calculating any polygonal number is represented as

m i= i+(k−2)(i−1)i/2

where m is a polygonal number, i is a serial number, k is the quantity of angles.

Thus, m 1=1; m 2=k; and for all other i the meaning of mi varies widely as shown in the following table:

Table 1. Polygonal numbers

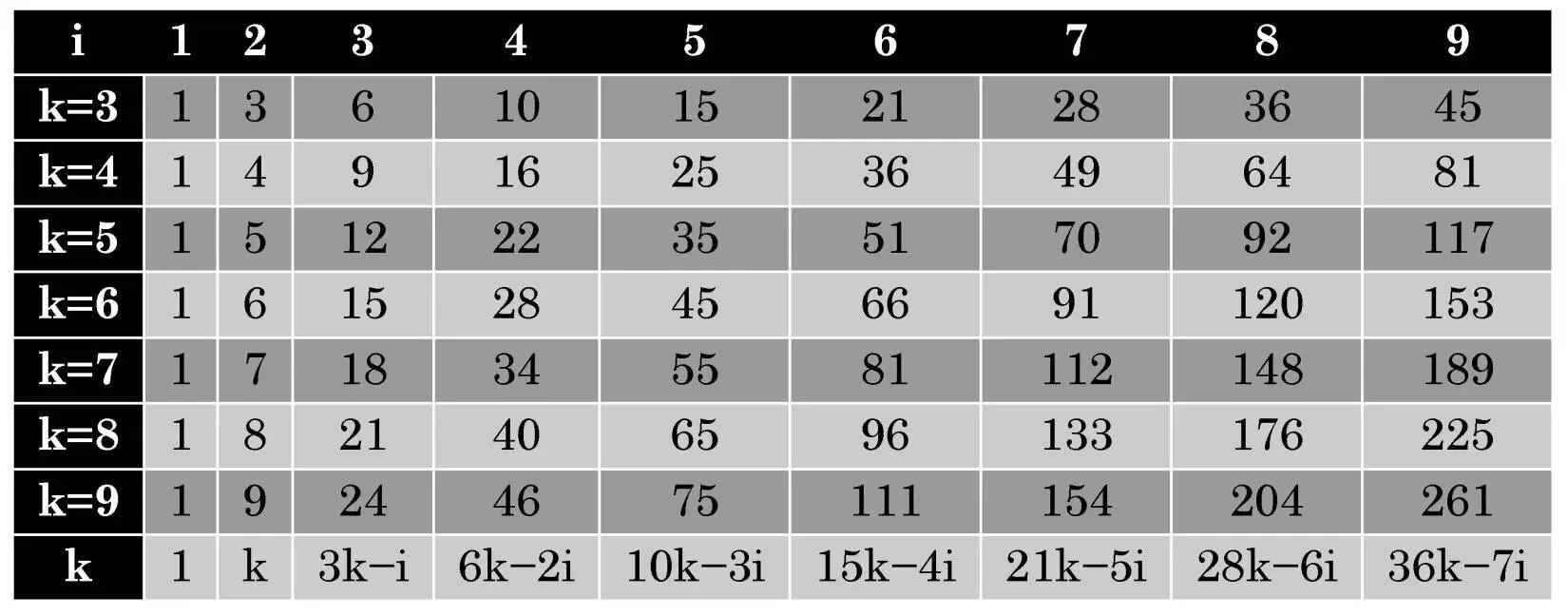
To calculate m iit is enough to obtain only triangular numbers by the formula, which is very easily since the difference between them grows by unit with each step. And all other m ican be calculated by adding the previous triangular number in the columns. For example, in column i=2, numbers increase by one, in column i=3 – by three, in column i=4 – by six etc. i.e. just on the value of the triangular number from the previous column.

To make sure that any natural number is represented by the sum of no more than k k-angle numbers is quite easily. For example, the triangular number 10 consists of one summand. Further 11=10+1, 12=6+6, 13=10+3 of two, 14=10+3+1 of three, 15 again of one summand. And so, it will happen regularly with all natural numbers. Surprisingly that the number of necessary summands is limited precisely by the number k. So, what is this miraculous power that invariably gives such a result?

As an example, we take a natural number 41. If as the summand triangular number will be closest to it 36, then it will not in any way to fit into three polygonal numbers since it consists minimum of 4 ones i.e. 41=36+3+1+1. However, if instead of 36 we take other triangular numbers for example, 41=28+10+3, or 41=21+10+10 then again in some unknown miraculous way everything will so as it stated in the FGT.

At first glance it seems simply unbelievable that it can somehow be explained? But we still pay attention to the existence of specific natural numbers, which are consisting at least of k k-angle numbers and denoted by us as S-numbers. Such numbers are easily to find for example, for triangles – 5, 8, 14, for squares – 7, 15, 23, for pentagons – 9, 16, 31 etc. And this our simple observation allows us directly to move to aim i.e. without using ingenious tricks or powerful "sharpness of mind".

Now to prove the FGT, suppose the opposite i.e. that there exists a certain minimal positive integer N consisting minimum of k + 1 k-angle numbers. Then it’s clear that this our supposed number should be between some k-angle numbers m iand m i+1and can be represented as

N=m i+δ 1where δ 1=N−m i(1)

It is quite obvious that δ 1must be an S-number since otherwise this would contradict our assumption about the number N. Then we proceed the same way as in our example with the number 41 i.e. represent the supposed number as

N = m i-1+δ 2where δ 2=N−m i-1

Now δ 2should also be an S-number. And here so we will go down to the very end i.e. before

δ i-1=N−m 2=N−k and δ i=N−m 1=N–1 (2)

Thus, in a sequence of numbers from δ 1to δ i, all of them must be S-numbers i.e. each of them will consist of a sum minimum of k k-angle numbers, while our supposed number N will consist minimum of k+1 k-angle numbers. From (1) and (2) it follows:

N− m i=S i(3)

Thus, if we subtract any smaller polygonal number m ifrom our supposed number N then according to our assumption, the result should be only an S-number. Of course, this condition looks simply unbelievable and it seems that we are already at target, but then how can one prove that this is impossible? …

If we gave an answer to this question here, then this famous Fermat's theorem would immediately turn into the most common school problem and interest to it would be lost. To prevent this from happening, we will stay on the fact that the proof is presented here only by 99% and the remaining 1% will be offered to those who will be interested in order to appreciate the true magnificence of this scientific achievement of Fermat, especially in comparison with the Cauchy’s GFT proof. 42

Pic. 34. Title Page the Cauchy's Proof

of the Fermat's Golden Theorem

Pic. 35. One of 43 Pages the Cauchy's Proof

of the Fermat's Golden Theorem

The problem statement is as follows:

Let any non-square number be given, you need to find an infinite number of squares, which after multiplication by this number and increasing by unit, will make a square .

Fermat proposed finding solutions for the numbers 61, 109, 149, and 433 [36].

The English mathematician John Wallis managed to find a way to calculate the required numbers using the Euclidean method of decomposing an irrational number into an infinite common fraction. He published his decision under the name "Commercium epistolicum" see pic. 37-38.