Алексей Ипатов - Православное научное мировоззрение

Есть и другая наглядная аналогия – перекрученная нитка. Можно даже не полениться и самостоятельно смоделировать: к нитке приклеить полоски-стрелочки, как зубья у расчёски. Пока нитку мы не крутим, все полоски-зубья смотрят в одну сторону. Начнём закручивать нитку. Полоски расположатся по спирали. А теперь мысленно устремляем толщину нитки к нулю и получим перекрученную прямую пространства.

Это мы попытались объяснить кручение точек пространства с помощью аналогии, можно даже сказать, что попытались представить. Теперь надо изложить этот же вопрос более научным языком, ибо аналогии и примеры не передают существенных особенностей. Элементарное вращение может происходить только в одной плоскости. Например, вращение вокруг оси z в привычном нам понимании есть поворот в плоскости x ^ y . Но, строго говоря, это только в трёхмерной геометрии поворот в плоскости однозначно выражается через поворот вокруг оси. Для пространства-времени можно спросить, «а почему не вокруг оси t ?» Описание вращения через плоскость, в которых находится изменяющийся угол, однозначно конкретизирует данное движение. Сложные виды вращений (поворот вокруг нескольких осей) раскладываются на сумму элементарных движений в разных плоскостях. В привычной нам геометрии пространства мы используем 3 координаты х, у, z . Трёх пространственных координат и времени t достаточно, чтобы иметь возможность однозначно обозначить любое событие в любой точке пространства в любой момент времени. Последняя фраза на научном языке звучит как "пространство событий". Для построения новой геометрии окружающего нас пространства с учётом ориентаций мы должны использовать уже 10 независимых размерностей: четыре линейные (трансляционные) координаты x , y , z , t и шесть угловых: углы в плоскостях между осями x ^ y , x ^ z , y ^ z и в плоскостях x ^ t , y ^ t , z ^ t. Можно сказать по-другому: из трёх привычных нам пространственных измерений мы получили десятимерное «пространство событий», т. е. набор из десяти параметров для каждого отдельного события "в данном месте в данное время".

Ранее мы "на пальцах", при помощи "самолётиков-точек" и их крена, рыскания и тангажа попытались объяснить, как возникает 10-мерное пространство событий. Теперь в нашем построении вместо самолётиков-точек будем использовать "ориентированную точку" или «единичный координатный базис».

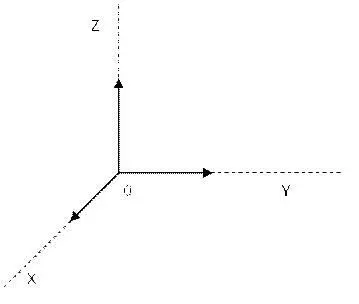
На первый взгляд, вроде бы всем знакомые оси координат. Но если говорить более точно – это всего-навсего одна ориентированная точка "0". Просто она никуда не повёрнута. Вектора её единичного базиса направлены вдоль осей координат. Возможна и другая ситуация:

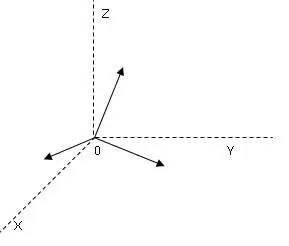
Та же самая точка "0", только повёрнутая относительно осей координат. Обратите внимание: оси координат показаны пунктиром, а стрелками – ориентация точки. Если кому-то из читателей будет понятнее: стрелки – это оси "самолётика". Как именно повёрнута это "ориентированная точка" = "самолётик" – по двумерному рисунку не сообразить.

В математике из множества точек получается прямая, из прямых – плоскость, из плоскостей – пространство. Поступим и мы также – соберём из этих "ориентированных точек"="единичных базисов" прямую (оси координат пунктиром уже не рисуем).

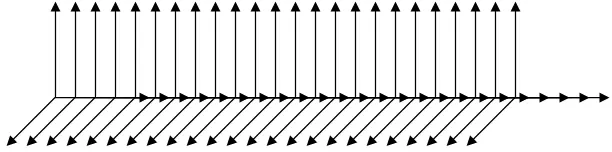
Из простых, никуда не повёрнутых точек получаем обычную банальную прямую.

А вот следующие случаи поинтереснее.

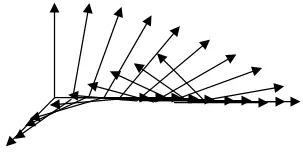
Поворот в плоскости y^z

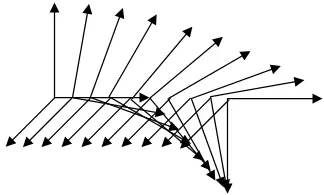
Поворот в плоскости x^z

Для лучшего представления кручёных прямых можно повторить наглядную аналогию. Перекрученная нитка с приклеенными полосками-стрелочками. С одной стороны, нитка прямая, т.е. без изгибов, с другой – она может быть вся закручена. Допустим, у некрученой нитки все стрелочки направлены вниз. При закручивании они уже будут менять своё направление. Если устремить толщину нитки к нулю, то и получим кручёную прямую с первого рисунка (y^z). Кручение в плоскости x^z со второго, равно как и аналогичное в плоскости x^y, аналогией наглядно не передать.

Надеемся, читатель и без рисунка сможет понять (а некоторые – даже представить), что возможно сочетание кручений в двух и в трёх плоскостях. Тоже несложно понять, что кручение вдоль прямой может быть разным:

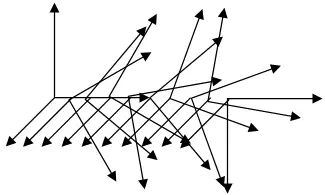
Неравномерное кручение в плоскости x^z.

На этом можно пока остановиться с пересказом новых научных достижений и попытаться подвести первый итог. Современные научные теории утверждают, что пространство и время в отсутствии вещества, силовых полей и элементарных частиц «сами по себе» обладают теми или иными свойствами, сходными со свойствами материи. До Эйнштейна была модель пространства, сотканного из бесконечного числа абсолютно твёрдых шариков, размеры которых стремятся к нулю. Из точек получают прямую, из прямых – плоскость, из плоскостей – пространство. Теория относительности «наделяет» шарики-точки пространства упругостью, они могут сплющиваться. Новый научный подход, помимо этого, предлагает ввести ещё три угловые величины: аналог тангажа, крена и рыскания для самолёта. Если перейти к пространству-времени, то получится уже 10: между 4 осями координат возможно 6 углов. В итоге получается "10-мерное пространство". При этом мы имеем все те же наши 3 пространственные координаты, время и 6 углов между ними.

Что мы сейчас уже можем сказать об этом новом поле кручений? Кстати, термин «поле кручений» используют достаточно редко. Почему-то русские учёные – первопроходцы чаще на английский манер говорят «спинорные» или «торсионные» поля. Теория предсказывает, что любые вращательные действия с материей, такие как вращение, перекручивание, спиральность и другие подобные приводят к возникновению какой-либо структуры в поле кручений. Видов такого вращения может быть очень много. Самое "глубинное" – спин элементарных частиц. Спин определяется наукой как квантовый аналог вращения. Все основные стабильные элементарные частицы, из которых состоит всё вещество: протон, нейтрон, электрон – обладают спином. Любая комбинация и любое движение этих основополагающих частиц вещества сопровождается «следом» в поле кручений. Кроме вращения как движения, существует множество статических вариантов создания структур поля кручений. Яркий пример – двойная спираль ДНК. Вращение может быть не только вещества, но и электромагнитного поля. Это и вращающиеся магнитное поле трёхфазного электродвигателя, и круговая поляризация излучения, и явление электромагнитной индукции. Наконец, может быть и макроскопическое вращение вещества. Из механических природных явлений укажем турбулентность и водовороты. Все эти и подобные им вращения порождают поле кручений «на своём уровне» или со своими параметрами.