Александр Харчевников - Матрица «обменов». Полилогия метаболизма

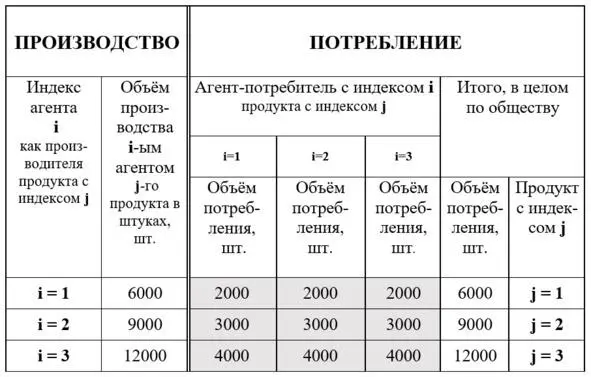
Рис. 8. Сокращённый вариант балансовой матрицы «производство-потребление», описывающей равновесное состояние общества, при условии равенства структур производства и потребления по каждому агенту и равенства самого воспроизводственного потребления этих агентов действительной жизни общества

Полученный результат достаточно тривиален и нагляден в отношении чисел, выражающих объёмы продуктов, а путь его получения повторяет четыре шага одного цикла кругооборота (обращения), указанные во введении к «Капиталу» в разделе «2. Общее отношение производства к распределению, обмену, потреблению» [13]. Эти шаги был подробно рассмотрены выше. В то же время с переходом к матрице рисунка 8 возникает некий казус с индексацией, в частности, с двойной индексацией анализируемых объёмов продуктов как элементов ячеек матрицы, которые по горизонтали (строка) связаны с координатой агента-производителя, а по вертикали (столбец) привязаны к координате агента-потребителя. Однако, так как каждый агент одновременно выступает в роли агента-производителя и агента-потребителя, то им присущ один и тот же индекс i, что вынуждает всё время оговаривать в какой роли выступает в данном моменте агент действительной жизни общества и вызывает затруднения в понимании изложенного, если такой оговорки нет. Общепринято, что первый индекс указывает всегда указывает строку, а второй индекс указывает на столбец данной матрицы. Иначе говоря, пара индексов ячеек с элементами матрицы, обозначающими количество продуктов, оказались обозначенными не только одинаковыми буквами « i», но при этом оказалась «утерянной» индексация вида продукта « j» ( j= 1, 2, …, q).

Для устранения этого казуса сохраним за первым индексом « i» первоначальное обозначение агента-производителя (строка), введя вместо обозначения второго индекса через « i» (столбец агента-потребителя) новое обозначение через « k». При этом сохраним индекс « j» для обозначения вида продукта. Тогда количество продукта в каждой ячейке матрицы, выделенной на рисунке 8 серым тонированием, будет иметь двойное индексирование с парой индексов « i» и « k», а сам элемент с количеством продукта в штуках будет обозначаться как – p ik( i = 1, 2, …, m; k= 1, 2, …, n). В данном примере максимальные значения индексов « i», « k» и « j» равны, соответственно, m= 3, n= 3 и q= 3.

С учётом сделанных изменений, оставляя решение вопроса о «потери» индекса « j» для последующего анализа, матричная таблица рисунка 8 примет вид, представленный на рисунке 9.

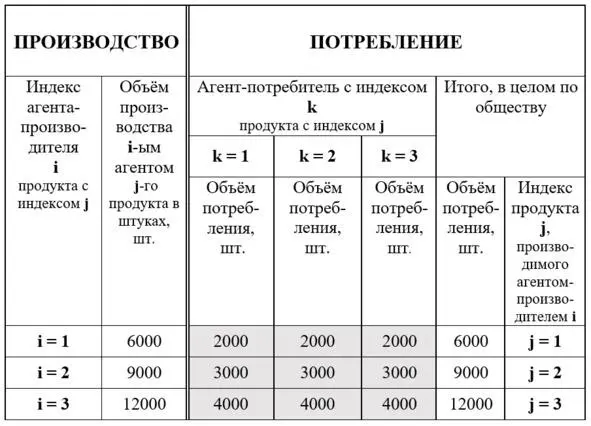
Рис. 9. Новый вариант балансовой матрицы «производство-потребление», описывающей равновесное состояние общества (при условии равенства структур производства и потребления по каждому агенту и равенства между собой самого воспроизводственного потребления этих агентов)

Рассмотрим собственно саму балансовую матрицу равновесного состояния (см. рис. 10), которая в таблице рисунка 9 выделена серым тонированием, вписав в неё дополнительно по каждому элементу условное обозначение количества продукта, обозначаемое двойной индексацией, – p ik.

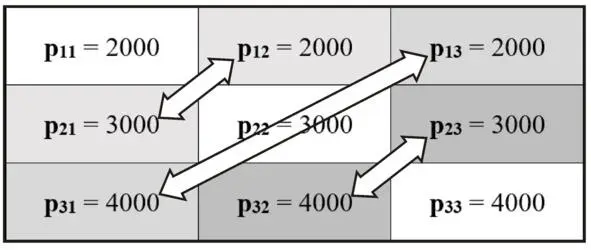
Рис. 10. Балансовая матрица «производство – потребление» в условиях равновесного состояния «условного общества»

На рисунке 10 двухсторонними фигурными стрелками соединены те элементы (ячейки) балансовой матрицы, агенты которых, как агенты-производители, вовлечены в «обмен», на что указывает «зеркальное» отображение индексов этих ячеек, точнее, индексов соответствующих объёмов потребления, то есть – p ik. Это следующие пары объёмов p ik:

Здесь, судя по зеркальному отображение двойных индексов, каждый из агентов выступает одновременно и как агент (первый индекс двойной индексации – i), отчуждающий свой продукт, и как агент (второй индекс двойной индексации – k), приобретающий для своего потребления продукт другого вида «взамен» отчуждённого продукта. В результате такого взаимодействия осуществляется метаболический «обменный» процесс, который в буржуазном обществе, в случае, если типологии обеих продуктов «внешний предмет, вещь», принято именовать «товарообменом». Ячейки матрицы с элементами этих пар, дополнительно к двухсторонним стрелкам, выделены тонировкой различной интенсивности, одинаковой для каждой пары.

Так, например, пара элементов p 12= 2000 и p 21= 3000 соединённых малой двухсторонней фигурной стрелкой и имеющих светло-серое тонирование соответствующих ячеек балансовой матрицы, последовательно читается следующим образом:

– Первый агент с индексом i = 1 отчуждает в пользу второго агента с индексом k = 2 2000 единиц (штук) произведённого им продукта с индексом j = 1,так как согласно матричной таблицы рисунка 9 только первый агент производит продукты с индексом j = 1 (и только этот продукт). При этом второй агент с индексом i = 2 отчуждает в пользу первого агента k = 1 3000 единиц (штук) произведённого им продукта с индексом j = 2,так как согласно матричной таблицы рисунка 9 только второй агент производит продукты с индексом j = 2 (и только этот продукт).

Следующая пара элементов p 13= 2000 и p 31= 4000, соединённых длинной двухсторонней фигурной стрелкой, последовательно читается следующим образом:

– Первый агент с индексом i = 1 отчуждает в пользу третьего агента с индексом k = 3 2000 единиц (штук) произведённого им продукта с индексом j = 1,так как согласно матричной таблицы рисунка 9 только первый агент производит продукты с индексом j = 1 (и только этот продукт). При этом третий агент i = 3 агент отчуждает в пользу первого агента k = 1 4000 единиц (штук) произведённого им продукта с индексом j = 3,так как согласно матричной таблицы рисунка 9 только третий агент производит продукты с индексом j = 3 (и только этот продукт).

Наконец, пара элементов p 23= 3000 и p 32= 4000, соединённых малой двухсторонней фигурной стрелкой и имеющих тёмное тонирование соответствующих ячеек балансовой матрицы, последовательно читается следующим образом: