Владимир Трошин - Слова и числа

G – множество гласных букв русского алфавита,

S – множество согласных букв,

P – множество полугласных букв,

Z – множество букв, которым не соответствует никакого звука в устной речи, иначе говоря – множество знаков,

D – множество звонких согласных,

T – множество глухих согласных,

X – множество шипящих согласных.

Бесконечное множество нельзя задать перечислением всех его элементов, но часто можно описать их свойства. Встречаются и конечные множества с той же степенью неопределенности. Например, до сих пор ученым не удалось расшифровать письменность острова Пасхи. До нас дошли несколько десятков табличек, покрытых рисуночными значками, вырезанными зубом акулы по дереву. Эти письмена аборигены называют кохау ронго-ронго – «говорящее дерево». Множество знаков-иероглифов в письменности острова Пасхи, можно определить этим предложением, но нельзя с уверенностью и точно перечислить, хотя это множество заведомо конечное.

Множества G , S , …, X содержат разное количество элементов и среди них есть одно, для которого используется специальное название. Множество, содержащее единственный элемент называется одноэлементным или единичным множеством . Речь идет о множестве P ={й}, которое содержит единственную букву, обозначающую полугласный звук, то есть звук не образующий слога. Можно задать и пустое множество , в котором не содержится ни одного элемента. Так как это множество никак не характеризуется своими отсутствующими элементами, то логично утверждать, что может быть только одно множество, не имеющее элементов. Для его обозначения принят специальный знак Ø.

Отношения между объектами и множествами описываются понятием принадлежности. Для записи этого отношения есть два специальных знака принадлежит и не принадлежит .

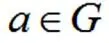
означает, что буква а – гласная и является элементом множества гласных букв, то есть принадлежит ему.

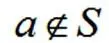
означает, что буква а не является согласной и не принадлежит множеству согласных букв. В качестве сокращения можно записывать отношение принадлежности сразу для нескольких элементов:

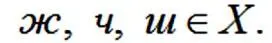
Отношения между множествами определяются следующими утверждениями.

Два множества равны в том и только в том случае, когда они состоят из одних и тех же элементов. Для обозначения равенства двух множеств применяется обычный знак равно {a, e, o}={e, o, a}. Порядок расположения элементов при их перечислении не важен, он не меняет состава множества.

Соответственно, два неравных множества отличаются, по крайней мере, одним своим элементом ( X ≠ {ж, ш, ч}).

Если каждый элемент множества А одновременно является элементом множества В , то говорят, что А включено в В или А есть подмножество множества В . Символически записывается:

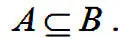
Выражение В содержит А является синонимом для выражения А включено в В .

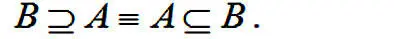
Если одновременно выполняются два условия: А включено в В и А ≠ В , то говорят, что множество А строго включено в В или А есть истинное подмножество множества В

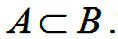
Пустое множество является подмножеством любого другого множества, то есть для любого множества А :

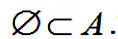
Знак включения как и знаки равенства и принадлежности имеет свое отрицание, которое выражается соответствующим перечеркнутым знаком, означающим, что А не является подмножеством множества В :

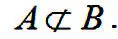
Применительно для ранее введенных буквенных множеств можно написать следующие утверждения:

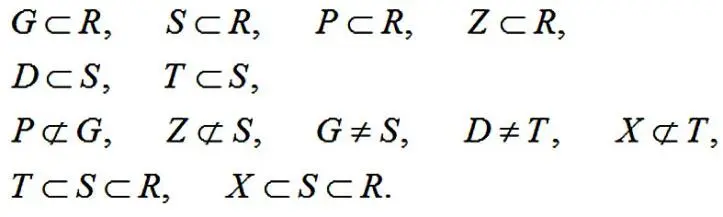
Попробуйте самостоятельно дать им словесную формулировку.

Каждое не пустое множество ( А ≠Ø) имеет по крайней мере два различных подмножества: само А и Ø. Кроме того, каждый элемент множества А определяет некоторое подмножество множества А . Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается P (А ).

Например, если С ={у, р, о, к}, то P ( С )= { С , {у, р, о}, {у, р, к }, {у, о, к}, {р, о, к}, {у, р}, {у, о}, {у, к}, {р, о}, {р, к}, {о, к}, {у}, {р}, {о}, {к}, Ø }.

Для конечного множества А , состоящего из n элементов, множество-степень P ( А ) содержит 2 n элементов. Действительно, в предыдущем примере мы получили 2 4=16 элементов.

Множества – это математические объекты и над ними можно выполнять некоторые операции.

Объединением множеств А и В называется множество всех предметов, которые являются элементами множества А или элементами множества В. Обозначается :

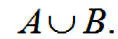
Слово или в этом определении имеет не исключающий, а собирательный смысл. Например, если мы объединим множество глухих согласных и множество звонких согласных, то получим множество всех согласных букв:

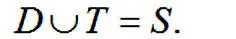
Справедлива и такая запись:

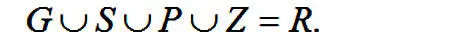
Пересечением множеств А и В называется множество всех предметов, являющихся элементами обоих множеств А и В одновременно. Обозначается :

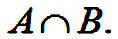
Среди звонких согласных есть только одна шипящая, буква – ж, а среди глухих три шипящих, поэтому:

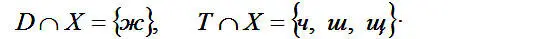
Два множества называются непересекающимися , если у них нет общих элементов:

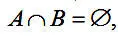
и пересекающимися , если

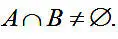
Множество гласных букв и множество согласных букв не имеют общих элементов – они непересекающиеся:

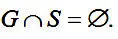
Дополнением множества А до множества В называется множество тех элементов множества В, которые не являются элементами множества А. Обозначается :