Владимир Гимпельсон - Транспортные проблемы мегаполисов

Утверждение [2], что в развитых городах мира площадь дорог занимает 20–30 % от площади города тоже является мифом. Такое соотношение может существовать в центре города, где здания окаймляются со всех сторон дорогами. Такое положение существует в Нью-Йорке, в центре Оттавы, внутри бульварного кольца Москвы. И в других местах вокруг каждого дома существуют проезды, необходимые для подъезда автомобилей и спецтехники. Площадь проездов может составлять значительную часть площади жилой застройки. Так что нужно четко определить, о площади каких дорог идет речь. Город и мегаполис не могут существовать без парков, лесных массивов, рек и водоемов. Поэтому дороги не могут занимать 20 % площади города. Да в этом и нет необходимости.

Если квадрат со стороной А окаймлен со всех сторон дорогами шириной b, площадь которых составляет 0.1 от площади квадрата, то есть 0,1*А 2=4A*b/2, то дороги шириной 7 м будут окаймлять квадраты со стороной 140 м.,

шириной 14 м будут окаймлять квадраты со стороной 280 м.,

шириной 35 будут окаймлять квадраты со стороной 700 м..

Последний пример соответствует наличию в Москве 21 кольца, как МКАД и 130 таких же радиальных дорог около МКАД (к центру число радиальных дорог будет уменьшаться). Трудно представить себе заторы при таком количестве дорог. На площади 100 км. 2могут одновременно двигаться с предельными скоростями 1 млн автомобилей, что составляет 20 % от парка автомобилей Москвы.

Но, быть может, в Москве нет такого количества дорог? Детальный расчет [5] показал, что в Москве в 2011 году площадь дорог составляла 89,7 км 3или 8.7 % от площади города. С 2011 по 2015 годы общая площадь объектов улично-дорожной сети и тротуаров в столице увеличилась [6] до 117 миллионов квадратных метров и общая длина дорог 6064 км. Ежегодно вводится свыше 100 км новых дорог. Реконструированы радиальные магистрали и почти все развязки на МКАД. Площадь МКАД увеличилась почти вдвое. Строятся хордовые магистрали. Но считается, что в Москве катастрофически мало дорог и потому заторы на дорогах – обычное явление.

Таблица 1. Основные магистрали Москвы

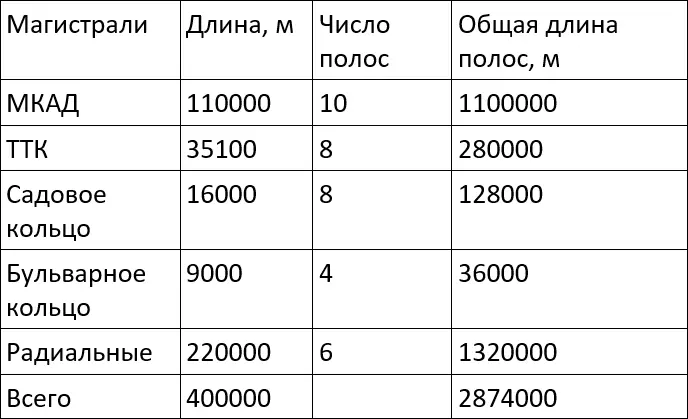
В Москве только около 6064 км дорог, а основных магистралей 400 км или 2874 км полос движения.

Проблема автомобильного трафика успешно решена в Токио. Но там построена многоуровневая радиально-кольцевая сеть дорог. Общая длина дорог в Токио составляет 28000 км (из них скоростных дорог 2800 км), а учитывая, что в Токио предпочитают строить 4-полосные дороги (шириной 14 м), число скоростных полос там 11 200 км и площадь дорог Токио составляет 392 км 2. При равномерной предельной загрузке по ней могли бы одновременно двигаться с максимальными допустимыми скоростями 3,9 млн автомобилей, то есть практически все автомобили города, а по скоростным дорогам только 390 000.

Следует заметить, что даже в Токио на каждый автомобиль не приходится 200 м 2, как утверждает М. Я. Блинкин, а меньше 100 м 2. Если любой путь в городе или при выезде за город связан с необходимостью использовать основные магистрали города, то их недостаток будет определять возможность перемещения по городу, как показано с помощью приведенного ниже расчета для Москвы.

Чтобы понять причину недостатка дорог в крупных городах и мегаполисах и ежедневных длительных заторов в Москве, следует обратить внимание на структуру дорог в Москве и большинства мегаполисов мира. Вдоль автомобильных и железных дорог возникали небольшие населенные пункты, которые разрастались в города с жилыми массивами, удаленными от междугородных дорог. От новых жилых массивов прокладывались дороги к уже существующим. Для пропуска увеличивающихся потоков автомобилей дороги расширялись. К ним прокладывали дороги от новых жилых массивов. Так возникала древовидная структура дорог. Дональд Дрю [7] считает необходимым иметь в городе дороги и улицы разного назначения. Улицы местного значения должны не только не учитывать требование сквозного движения, но в некоторых случаях умышленно препятствовать ему. Магистральные улицы городского значения и скоростные дороги, являющиеся продолжением внегородских автострад, должны служить путями транзитного движения. Районные и местные магистрали могут служить для выезда из улиц в общегородские магистрали.

Есть мнение [2], что общественный транспорт не должен ходить по дорогам, а только по улицам.

Древовидная структура дорог приводит к большим перепробегам при поездках между районами города, так как при любой поездке нужно из улицы выехать в местную магистраль, затем в районную, городскую, в другую районную, местную магистраль и, наконец в улицу пункта назначения. Это приводит к значительному увеличению времени пребывания в пути.

При этом нельзя согласиться с Михаилом Блинкиным [2] что в Москве коффициент перепробега, то есть отношение реального пути между двумя пунктами к длине прямой, соединяющей эти пункты, составляют громадную величину 1.53 и что в прямоугольной системе дорог он значительно меньше – 1,2, а при наличии хордовых дорог еще меньше и что радиально – кольцевая система дорог является тупиковой и годится только для устройства средневековых крепостей [1]. Это утверждение из уст авторитетного человека воспринято многими как абсолютная истина и осела в сознании многих людей. Однако все эти утверждения ложны, что легко понять, если вспомнить школьную геометрию. Два катета равнобедренного прямоугольного треугольника в 1.42 раза длинее гипотенузы. Таков будет перепробег при пересечении города по диаметру, совпадающему с гипотенузой, но двигаясь по катетам при геометрически идеальной прямоугольной структуре дорог. Если двигаться по катетам не равнобедренного треугольника для перемещения между двумя точками города, то разница будет меньше. Если ваш путь совпадет с одним из катетов, то путь будет кратчайшим. В радиально-кольцевой геометрически идеальной структуре дорог путь при пересечение города по диаметру будет кратчайшим. При движении между двумя произвольными точками можно избрать путь по одной из радиальных дорог и по луге меньшего радиуса, тогда путь будет меньше, чем в прямоугольной системе дорог. Но в реальном городе, как правило, идеально прямых дорог мало и движение даже по одной из них больше кратчайшего расстояния «по воздуху». Но дело обстоит гораздо хуже из – за низкой связности дорог.

Речь идет не только о проблеме выезда из района, из которого выходит только одна дорога. Выехать из такого района может быть проблематично, если на этой единственной дороге произойдет ДТП или дорогу перекроет товарный поезд.