Дмитрий Гусев - Краткий курс логики: Искусство правильного мышления

Юпитер движется. Марс движется. Венера движется. Юпитер, Марс, Венера – это планеты. Все планеты движутся.

Первые три посылки представляют собой частные случаи, четвёртая посылка подводит их под один класс объектов, объединяет их, а в выводе говорится обо всех объектах этого класса, т. е. формулируется некое общее правило (вытекающее из трёх частных случаев). Легко увидеть, что индуктивные умозаключения строятся по принципу, противоположному построению дедуктивным умозаключениям. В индукции рассуждение идёт от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, в отличие от дедуктивных, не достоверны, а вероятностны. В рассмотренном выше примере индукции признак, обнаруженный у некоторых объектов какой-то группы, перенесён на все объекты этой группы, сделано обобщение, которое почти всегда чревато ошибкой: вполне возможно наличие в группе каких-то исключений, и даже если множество объектов из некой группы характеризуется каким-то признаком, то это не означает с достоверностью, что таким признаком характеризуются все объекты данной группы. Вероятностный характер выводов является, конечно же, недостатком индукции. Однако её несомненное достоинство и выгодное отличие от дедукции, которая представляет собой сужающееся знание, заключается в том, что индукция – это расширяющееся знание, способное приводить к новому, в то время как дедукция – это разбор старого и уже известного.

3. Умозаключения по аналогии (аналогия)(от греч. analogia – соответствие) – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь. Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода. Вероятно, на Марсе есть жизнь.

Как видим, сравниваются (сопоставляются) два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в Солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.

1. Что представляет собой умозаключение? Почему посылки умозаключения должны быть истинными и связанными между собой суждениями?

2. Чем отличаются непосредственные умозаключения от опосредованных? Приведите по три примера непосредственных и опосредованных умозаключений.

3. Что представляют собой дедуктивные умозаключения? Почему выводы дедукции достоверны?

4. Что такое индуктивные умозаключения? Чем отличается индукция от дедукции? В чём причина вероятностного характера индуктивных выводов?

5. Каким образом строятся умозаключения по аналогии? Чем они отличаются от дедуктивных и индуктивных умозаключений?

Все дедуктивные умозаключения называются силлогизмами(от греч. sillogismos – подсчитывание, подытоживание, выведение следствия). Существует несколько видов силлогизмов. Первый из них называется простым( категорическим), потому что все входящие в него суждения (две посылки и вывод) являются простыми, или категорическими. Это уже известные нам суждения видов A , I , E , O .

Рассмотрим пример простого силлогизма:

Все цветы ( М ) – это растения ( Р ).

Все розы ( S ) – это цветы ( М ).

Все розы ( S ) – это растения ( Р ). Обе посылки и вывод являются в данном силлогизме простыми суждениями (причём и посылки, и вывод – это суждения вида A (общеутвердительные)). Обратим внимание на вывод, представленный суждением: « Все розы – это растения ». В этом выводе субъектом выступает термин « розы », а предикатом – термин « растения ». Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин « цветы », который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщённые в посылках термины « растения » и « розы » можно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трёх (различным образом расположенных) терминов:

1. Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма(вторая посылка также называется меньшей).

2. Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма(первая посылка также называется большей). Предикат вывода, как правило, является по объёму большим понятием, чем субъект вывода (в приведённом примере понятия « розы » и « растения » находятся в отношении родовидового подчинения), в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.

3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизмаи обозначается латинской буквой М , потому что «средний» на латинском – это medium .

Три термина силлогизма могут быть расположены в нём по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т. е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

Первая фигура силлогизма– это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

Все газы ( М ) – это химические элементы ( Р ).

Гелий ( S ) – это газ ( М ).

Гелий ( S ) – это химический элемент ( Р ). Учитывая, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведённом примере (рис. 34):

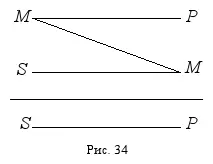
Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, отношения между тремя терминами можно изобразить с помощью кругов Эйлера. В данном случае получится следующая схема (рис. 35):