Дмитрий Гусев - Краткий курс логики: Искусство правильного мышления

1. О чём говорит закон противоречия? Объясните, почему этот закон не действует, если речь идёт о разных объектах, в разное время и в различном отношении. Проиллюстрируйте действие закона противоречия с помощью какого-нибудь самостоятельно подобранного примера. Какая тождественно-истинная формула является выражением закона противоречия?

2. Если логический принцип непротиворечивости мышления настолько прост и очевиден, то почему он возводится в ранг одного из основных законов логики?

3. Что такое контактные и дистантные противоречия? Придумайте по одному примеру контактных и дистантных противоречий.

4. Что такое явные и неявные противоречия? Придумайте по одному примеру явных и неявных противоречий. Почему дистантные и неявные противоречия встречаются в интеллектуально-речевой практике намного чаще, чем контактные и явные?

5. На какие четыре группы можно разделить все противоречия?

Найдите в художественной, публицистической, научной и учебной литературе по одному примеру для следующих видов противоречий: контактных и неявных, дистантных и явных, дистантных и неявных.

6. Что такое мнимые противоречия? Приведите два или три примера мнимых противоречий (за исключением тех, которые были рассмотрены в параграфе). Подумайте, почему мнимое противоречие часто используется в качестве художественного приёма?

7. В известной песне «Подмосковные вечера» есть такие слова:

«… речка движется и не движется… песня слышится и не слышится…». Реальное или мнимое противоречие представляет собой эта фраза? Обоснуйте свой ответ.

8. Все помнят знаменитые слова из сказки Александра Сергеевича Пушкина: « Кто на свете всех милее, всех румяней и белее? » Возможно, вы и раньше задумывались над тем, как можно быть румяней и белее одновременно. Реальное или мнимое противоречие присутствует в данном высказывании? Обоснуйте свой ответ.

9. Могут ли два суждения, одно из которых что-либо утверждает, а другое то же самое отрицает об одном и том же предмете, в одно и то же время и в одном и том же отношении, быть одновременно ложными? Если могут, то приведите несколько примеров таких суждений.

Суждения бывают противоположными и противоречащими. Например, суждения: « Сократ высокий », « Сократ низкий », – являются противоположными, а суждения: « Сократ высокий », « Сократ невысокий », – противоречащими. В чём разница между противоположными и противоречащими суждениями? Нетрудно заметить, что противоположные суждения всегда предполагают некий третий, средний, промежуточный вариант. Для суждений: «Сократ высокий», «Сократ низкий» , – третьим вариантом будет суждение: «Сократ среднего роста». Противоречащие суждения, в отличие от противоположных, не допускают или автоматически исключают такой промежуточный вариант. Как бы мы ни пытались, мы не сможем найти никакого третьего варианта для суждений: «Сократ высокий», «Сократ невысокий» (ведь и низкий, и среднего роста - это всё невысокий).

Именно в силу наличия третьего варианта противоположные суждения могут быть одновременно ложными. Если суждение: «Сократ среднего роста» , – является истинным, то противоположные суждения: «Сократ высокий», «Сократ низкий» , – одновременно ложны.

Точно так же именно в силу отсутствия третьего варианта противоречащие суждения не могут быть одновременно ложными. Таково различие между противоположными и противоречащими суждениями. Сходство между ними заключается в том, что и противоположные суждения, и противоречащие не могут быть одновременно истинными, как того требует закон противоречия. Таким образом, этот закон распространяется и на противоположные суждения, и на противоречащие. Однако, как мы помним, закон противоречия запрещает одновременную истинность двух суждений, но не запрещает их одновременную ложность; а противоречащие суждения не могут быть одновременно ложными, т. е. закон противоречия является для них недостаточным и нуждается в каком-то дополнении. Поэтому для противоречащих суждений существует закон исключённого третьего, который говорит о том, что два противоречащих суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными (истинность одного из них обязательно означает ложность другого, и наоборот). Символическая запись закона исключённого третьего представляет собой следующую тождественно-истинную формулу: a 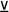¬ a (читается – «а или не а»), где a – это какое-либо высказывание.

1. В чём различие между противоположными и противоречащими суждениями? Почему противоположные суждения могут быть одновременно ложными, а противоречащие – не могут?

2. В чём сходство между противоположными и противоречащими суждениями? Почему закон противоречия является недостаточным для противоречащих суждений и нуждается в дополнении?

3. О чём говорит закон исключённого третьего? Какая тождественно-истинная формула является его выражением? В каком отношении находится закон исключённого третьего к закону противоречия?

Закон достаточного основанияутверждает, что любая мысль (тезис) для того, чтобы иметь силу, обязательно должна быть доказана (обоснована) какими-либо аргументами (основаниями), причём эти аргументы должны быть достаточными для доказательства исходной мысли, т. е. она должна вытекать из них с необходимостью (тезис должен с необходимостью следовать из оснований).

Приведём несколько примеров. В рассуждении: «Это вещество является электропроводным (тезис), потому что оно – металл (основание)», – закон достаточного основания не нарушен, так как в данном случае из основания следует тезис (из того, что вещество металл, вытекает, что оно электропроводно). А в рассуждении:

«Сегодня взлётная полоса покрыта льдом (тезис), ведь самолёты сегодня не могут взлететь (основание)», – рассматриваемый закон нарушен, тезис не вытекает из основания (из того, что самолёты не могут взлететь, не вытекает, что взлётная полоса покрыта льдом, ведь самолёты могут не взлететь и по другой причине). Так же нарушается закон достаточного основания в ситуации, когда студент говорит преподавателю на экзамене: «Не ставьте мне двойку, спросите ещё (тезис) , я же прочитал весь учебник, может быть, и отвечу что-нибудь (основание)». В этом случае тезис не вытекает из основания (студент мог прочитать весь учебник, но из этого не следует, что он сможет что-то ответить, так как он мог забыть всё прочитанное или ничего в нём не понять и т. п.).