Дмитрий Гусев - Краткий курс логики: Искусство правильного мышления

Видовые и родовые понятия тесно связаны между собой логическими операциями ограничения и обобщения.

Ограничение понятия– это логическая операция перехода от родового понятия к видовому с помощью прибавления к его содержанию какого-либо признака (или нескольких признаков).

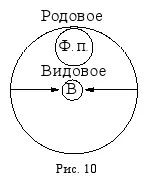
Вспомним об обратном отношении между объёмом и содержанием понятия: чем больше объём, тем меньше содержание, и наоборот. Ограничение понятия, или переход от родового понятия к видовому – это уменьшение его объёма, а значит – увеличение содержания. Вот почему при добавлении каких-либо признаков к содержанию понятия автоматически уменьшается его объём. Например, если к содержанию понятия « физический прибор » (Ф. п.) прибавить признак « измерять напряжение электрического тока », то оно превратится в понятие « вольтметр » (В), которое будет видовым по отношению к исходному родовому понятию « физический прибор » (рис. 10).

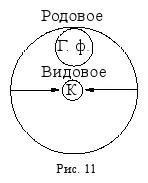
Так же, если к содержанию понятия « геометрическая фигура » (Г. ф.) прибавить признак « иметь равные стороны и прямые углы », то оно превратится в понятие « квадрат » (К), которое будет видовым по отношению к исходному родовому понятию « геометрическая фигура » (рис. 11).

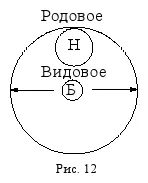
Обобщение понятия– это логическая операция перехода от видового понятия к родовому с помощью исключения из его содержания какого-либо признака (или нескольких признаков). Содержание понятия, лишённое каких-то признаков, уменьшается, но при этом автоматически увеличивается объём понятия, которое из видового становится родовым или обобщается. Например, если от содержания понятия « биология » (Б) отбросить признак « изучать различные формы жизни », то оно превратится в понятие « наука » (Н), которое будет родовым по отношению к исходному видовому понятию « биология » (рис. 12).

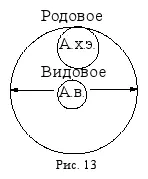
Так же, если от содержания понятия « атом водорода » (А. в.) отбросить признак « иметь один электрон », то оно превратится в понятие « атом химического элемента » (А. х. э.), которое будет родовым по отношению к исходному видовому понятию « атом водорода » (рис. 13).

Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие « Солнце », то получится следующая цепочка: Солнце → звезда → небесное тело → → физическое тело → форма материи . В этой цепочке понятие « звезда » является родовым по отношению к понятию « Солнце », но видовым по отношению к понятию « небесное тело »; так же понятие « небесное тело » является родовым по отношению к понятию « звезда », но видовым по отношению к понятию « физическое тело » и т. д. Движение по нашей цепочке от понятия «Солнце» к понятию « форма материи » представляет собой серию последовательных обобщений, а движение в обратном направлении – серию ограничений. Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький будет обозначать понятие « Солнце », а самый большой – « форма материи ».

Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие (см. раздел 1.1.), а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие, например: объект мироздания, форма материи или форма бытия .

Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некого целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части. Например, в качестве ограничения понятия « цветок » предлагают понятие « стебель ». Действительно, стебель – это часть цветка, но ограничить понятие – значит подобрать не часть для целого, а вид для рода. Следовательно, правильным ограничением понятия « цветок » будет понятие « ромашка », или « тюльпан », или « хризантема » и т. п. В качестве обобщения понятия « дерево » нередко предлагают понятие « лес ». Конечно же, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить понятие – значит подобрать не целое для части, а род для вида. Следовательно, правильным обобщением понятия « дерево » будет понятие « растение », или « объект флоры », или « живой организм » и т. п.

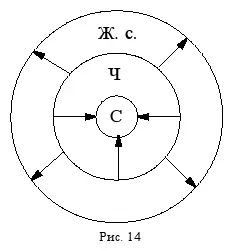
Итак, почти любое понятие (за исключением единичных и широких, философских) можно как ограничить, так и обобщить. Другими словами, подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия « человек » (Ч) будет понятие « спортсмен » (С) или « писатель », или « мужчина », или « молодой человек » и т. п., а его обобщением будет понятие « живое существо » (Ж. с.) (рис. 14).

1. Что такое ограничение понятия?

2. Что представляет собой логическая операция обобщения понятия?

3. Каким образом ограничения и обобщения понятий складываются в логические цепочки? Каковы пределы цепочек ограничений и обобщений?

4. Какие ошибки часто допускают при ограничении и обобщении понятий? Продемонстрируйте на самостоятельно подобранных примерах, что целое и часть нельзя путать с видом и родом.

5. Всякое ли понятие можно подвергнуть ограничению или обобщению? Какие понятия не поддаются этим логическим операциям?

6. Подберите десять любых понятий и проделайте с ними ограничение и обобщение, т. е. подберите для каждого как видовое, так и родовое понятие, иллюстрируя эти операции схемами Эйлера.

Определение понятия– это логическая операция, которая раскрывает содержание понятия.

Определения бывают явными и неявными.

Явноеопределение непосредственно раскрывает содержание понятия, даёт прямой ответ на вопрос, чем является объект, который оно обозначает. Например: « Термометр – это физический прибор, предназначенный для измерения температуры », – явное определение.