Джеймс Глейк - Хаос. Создание новой науки

Особый вид движения жидкости породил три уравнения Лоренца, которые описывают течение газа или жидкости, известное как конвекция. В атмосфере конвекция как бы перемешивает воздух, нагретый при соприкосновении с теплой почвой. Можно заметить, как мерцающие конвекционные волны поднимаются, подобно привидениям, над раскаленным асфальтом или другими поверхностями, излучающими теплоту. Лоренц испытывал искреннюю радость, рассказывая о конвекции горячего кофе в чашке. По его утверждению, это один из бесчисленных гидродинамических процессов в нашей Вселенной, поведение которых нам, вероятно, захочется предугадать. Как, например, вычислить, насколько быстро остывает чашка кофе? Если напиток не слишком горячий, теплота рассеется без всякого гидродинамического движения, и жидкость перейдет в стабильное состояние. Однако если кофе горячий, конвекция повлечет перемещение жидкости с большей температурой со дна чашки на поверхность, где температура ниже. Этот процесс наблюдается особенно отчетливо, если в чашку с кофе капнуть немного сливок — тогда видишь, сколь сложно кружение жидкости. Впрочем, будущее состояние подобной системы очевидно: движение неизбежно прекратится, поскольку теплота рассеется, а перемещение частиц жидкости будет замедлено трением. Как поясняет Лоренц, «у нас могут быть трудности с определением температуры кофе через минуту, но предсказать ее значение через час нам уже гораздо легче». Формулы движения, определяющие изменение температуры кофе в чашке, должны отражать будущее состояние этой гидродинамической системы. Они должны учитывать эффект рассеивания, при котором температура жидкости стремится к комнатной, а ее скорость — к нулю.

Отталкиваясь от совокупности уравнений, описывающих конвекцию, Лоренц как бы разобрал их на части, выбросив все, что могло показаться несущественным, и таким образом значительно упростил систему. От первоначальной модели не осталось почти ничего, кроме факта нелинейности. В результате уравнения, на взгляд физика, приобрели довольно простой вид. Взглянув на них — а это делал не один ученый на протяжении многих лет, — можно было с уверенностью сказать: «Я смог бы их решить».

Лоренц придерживался иного мнения: «Многие, увидев такие уравнения и заметив в них нелинейные элементы, приходят к выводу, что при решении эти элементы несложно обойти. Но это заблуждение».

Рассмотрим простейший пример конвекции. Для этого представим некоторый замкнутый объем жидкости в сосуде с ровным дном, который можно нагревать, и с гладкой поверхностью, подвергающейся в ходе опыта охлаждению. Разница температур между горячим дном и прохладной поверхностью порождает токи жидкости. Если разница небольшая, жидкость остается неподвижной; теплота перемещается к поверхности благодаря тепловой проводимости, как в металлическом бруске, не преодолевая естественное стремление жидкости находиться в покое. К тому же такая система является устойчивой: случайные движения, происходящие, например, когда лаборант нечаянно заденет сосуд, обычно замирают, и жидкость возвращается в состояние покоя.

Но стоит увеличить температуру, как поведение системы меняется. По мере нагревания жидкости она расширяется снизу, становится менее плотной, что, в свою очередь, влечет уменьшение ее массы, достаточное, чтобы преодолеть трение; в результате вещество устремляется к поверхности. Если конструкция сосуда хорошо продумана, в нем появляется цилиндрический завиток, в котором горячая жидкость поднимается по одной из стенок, а охлажденная спускается по противоположной.

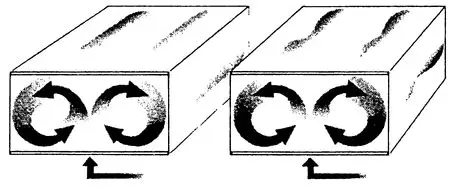
Рис. 1.2. Движение жидкости. Когда жидкость нагревают снизу, то в ней обычно образуются цилиндрические завитки (слева). Поднимаясь по одной стенке сосуда и спускаясь затем по противоположной, жидкость теряет теплоту — наблюдается конвекция. В случае продолжения этого процесса возникает нестабильность, влекущая за собой колебания в завитках жидкости, идущие в двух направлениях по всей длине цилиндров. При повышении температуры поток становится бурным и беспорядочным.

Понаблюдав за сосудом, можно проследить непрерывный цикл таких перемещений. Вне лабораторных стен сама природа создает области конвекции. К примеру, когда солнце нагревает песчаную поверхность пустыни, перемещающиеся воздушные массы могут сформировать миражи высоко в облаках или вблизи земли.

С дальнейшим ростом температуры поведение жидкости еще больше усложняется: в завитках зарождаются колебания. Уравнения Лоренца были слишком примитивными для их моделирования, описывая лишь одну черту, характерную для конвекции в природе, — кругообразное перемещение нагретой жидкости, показанное на рис. 1.2. В уравнениях учитывалась как скорость такого перемещения, так и теплопередача; и оба физических процесса взаимодействовали. Подобно любой циркулирующей частице горячей жидкости, жидкое вещество в нашем опыте, взаимодействуя с менее нагретой субстанцией, утрачивает теплоту. Однако, если движение жидкости происходит достаточно быстро, она не потеряет всю избыточную тепловую энергию за один цикл перемещений «дно —> поверхность —> дно», и в этом случае в ней могут образоваться завихрения.

Оказалось, что система Лоренца имеет аналоги в реальном мире, даже не отражая полностью процесс конвекции. К примеру, уравнения Лоренца достаточно точно описывают функционирование уже вышедшей из употребления электрической динамо-машины, предшественницы современных генераторов, где ток течет через диск, вращающийся в магнитном поле. В определенных условиях динамо-машина может дать обратный ход. Некоторые ученые, ознакомившись с уравнениями Лоренца, предположили, что, быть может, поведение динамо прольет свет на другой специфический феномен — магнитное поле Земли. Известно, что так называемая гео-динамо-машина давала о себе знать много раз в истории планеты. Интервалы между этими явлениями казались странными и необъяснимыми. Столкнувшись с подобной беспорядочностью, теоретики, как правило, искали решение вне рамок конкретной системы, выдвигая предположения вроде гипотезы метеоритных дождей.

Другой системой, вполне точно описываемой уравнениями Лоренца, является водяное колесо определенного типа, механический аналог вращающихся конвекционных кругов. Вода постоянно льется с вершины колеса в емкости, закрепленные на его ободе, а из каждой емкости она вытекает через небольшое отверстие. В том случае, когда поток воды мал, верхние емкости заполняются недостаточно быстро для преодоления трения. Если же скорость водяной струи велика, колесо начинает поворачиваться под воздействием веса жидкости и вращение становится непрерывным. Однако, коль скоро струя сильна, черпаки, полные воды, некоторое время колеблются внизу, а затем начинают стремиться в другую сторону, таким образом замедляя движение, а затем останавливая колесо; и в дальнейшем оно меняет направление движения на противоположное, поворачиваясь сначала по часовой стрелке, а потом — против нее.