Колин Уилсон - Боги Атлантиды

Плантар оказался радушным и галантным пожилым джентльменом (он родился в 1920 году). Он прибыл с группой последователей, из которых выделялся его товарищ маркиз Филип де Шеризе. Линкольн узнал о том, что именно Шеризе создал большую часть Секретных Досье, помещенных в Лувр. Линкольн обрадовался, заметив, как все они напряглись, когда на экране появился один из пергаментов, на котором было изображено нечто вроде пентаграммы.

Линкольн уже обратил внимание на странную геометрию картины Пуссена «Аркадские пастухи». Он искал секрет, который мог встревожить Людовика XIV, и заметил, что посох того пастуха, что стоит справа, разделен его рукой на две половины, а расстояние между верхним концом посоха и указательным пальцем пастуха равно той же «половинной величине». Вскоре он увидел, что на полотне таких «половинных величин» много. Художник, вне всякого сомнения, продумал ее геометрию.

Линкольн показал картину профессору Кристоферу Корнфорду из Королевского колледжа искусств. Корнфорд сделал ошеломляющее открытие: композиция картины базируется на геометрической пропорции, известной как «золотое сечение» (оно обозначается греческой буквой «фи»).

На первый взгляд мы столкнулись со скучным определением из школьного учебника геометрии, но золотое сечение так широко распространено и столь любопытно, что ему стоило бы посвятить отдельную книгу. Если коротко, оно описывает деление отрезка на две части, при котором длины короткой и длинной частей соотносятся так же, как длины длинной части и всего отрезка, как показано на рисунке.

Эта задача кажется головомкой из тех, которыми изобилуют занимательные книги для детей. Чем же интересно золотое сечение?

Тем, что по непонятной причине оно очень часто встречается в природе. Возьмите ваше тело: пупок делит его на две части именно в такой пропорции. Этому соотношению подчиняются узор на листе, лепестки цветка, листья на ветке, годовые кольца деревьев, семена в головке подсолнуха, морские раковины, даже рукава спиральных туманностей.

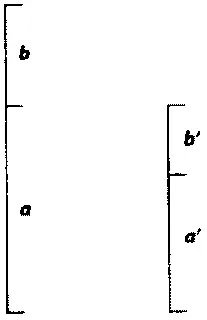
Золотое сечение

Художники используют золотое сечение, когда делают наброски, поскольку композиция картины, подчиняющаяся этому соотношению, радует глаз так же, как музыкальная гармония услаждает слух.

Почему природе нравится золотое сечение? Потому что это наилучший способ упаковать нечто, минимизировав занимаемое этим «нечто» пространство.

Может показаться, что золотое сечение описывается незамысловатой дробью, но это не так: в десятичном виде эта дробь 0,618034… продолжается до бесконечности.

В другой форме «фи» приближенно равно 1,618. Если вам нужно удлинить отрезок сообразно золотому сечению, просто умножьте его длину на 1,618.

Прежде чем вернуться к загадке Ренн-ле-Шато, еще немного математики. Существует названный по имени математика Фибоначчи ряд чисел, в котором каждое последующее число равно сумме двух предыдущих. Если начать с 0, следующим числом будет 1, затем 0+1 даст нам 1. Затем, если прибавить 1 к 1, мы получим 2. Прибавив 2 к 1, получим 3\И так далее (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…).

Вот еще один интересный факт. Если взять два соседних числа Фибоначчи и разделить меньшее на большее, чем больше будут числа, тем ближе частное будет к золотому числу 0,618034… Например, если 2 разделить на 3, получится 0,6666… Но если 34 разделить на 55, получим 0,6182. Неважно, насколько велики числа Фибоначчи, пусть даже это будут миллионы и миллиарды, частное никогда не станет точно равно золотому числу.

Именно числа Фибоначчи можно обнаружить в годичных кольцах деревьев, раковинах моллюсков, спиральных туманностях. Почему Богу нравится золотое число — никто не знает. Стоит упомянуть о том, что спираль Фибоначчи можно вывести из пентакля. Если часть внутренней пентаграммы поместить под прямым углом к «ногам» пентакля, можно описать спираль Фибоначчи, начав с конца короткой линии.

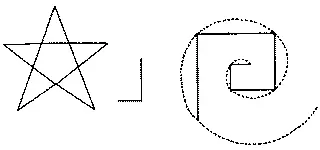
Спираль Фибоначчи

Кажется, Богу почему-то нравятся пентаграммы! Стоит добавить также, что, согласно Геродоту (в тексте, который мы немного подправим, устранив ошибку переписчика, делающую его абсурдным), золотое сечение можно найти в каждой грани пирамиды Хеопса.

Корнфорд объяснил Линкольну, что, изучая «Аркадских пастухов», искал одну из двух систем, которые постоянно использовали художники в ту эпоху. Первая — это система чисел, основанная на диалоге Платона «Тимей» (повествующем о создании вселенной) и очень популярная в эпоху Ренессанса. Вторая — куда более древняя геометрическая система, в основе которой лежит золотое сечение.

Корнфорд рассчитывал обнаружить на полотне Пуссена систему «Тимея», поскольку система золотого сечения считалась тогда ужасно старомодной. Он обнаружил следы системы чисел, но в общем и целом «Аркадские пастухи» базируются на золотом сечении. Кроме того, на картине скрыто множество пятиугольников.

Посмотрим вот на этот рисунок:

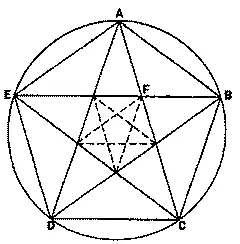
Пентаграмма в круге

Отношение каждой из пяти сторон пентаграммы (например, АВ) к ее хордам (скажем, АС) равно 1:1,618, или «фи».

Приглядевшись, Корнфорд обнаружил, что может нарисовать пентаграмму, которая выйдет за рамки картины:

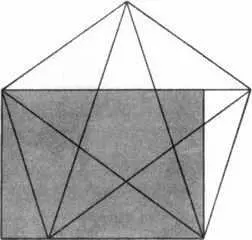
Пентаграмма, расширенная за рамки «Аркадских пастухов»

Если коротко, в картине Пуссена зашифрован пентакль. В итоге Корнфорд сделал любопытное замечание: возможно, фраза «у Пуссена есть ключ…» относится к местности вокруг Ренн-ле-Шато, где Соньер искал свои сокровища?

Это замечание привело Линкольна к одному из его важнейших открытий.

Бросив взгляд на топографическую карту окрестностей Ренн-ле-Шато, он сразу отметил, что три крупнейших населенных пункта (Ренн-ле-Шато, тамплиерский замок Безю и замок Бланшфор) являются тремя вершинами треугольника. Все они расположены на холмах.

Нарисовав на карте треугольник, Линкольн измерил его стороны и изумился. Треугольник получился идеально равнобедренным, проще говоря, две из трех его сторон оказались равны. Замок Безю располагается в вершине треугольника, от замка Бланшфор и от Ренн-ле-Шато его отделяет одно и то же расстояние.

Вряд ли это совпадение. Очень давно кто-то заметил, что вершины трех холмов образуют равнобедренный треугольник, и решил, что они подходят для некоего тайного замысла.