Вашингтон Плэтт - Информационная работа стратегической разведки. Основные принципы

Степень дисперсии может определяться различными путями: путем учета амплитуды, среднего квадратичного отклонения, среднего отклонения, вероятной ошибки и т. д. Соответствующие определения и формулы можно найти в любой книге по математической статистике (см. список литературы в конце книги).

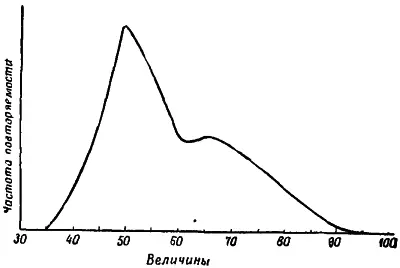
Если результаты изучения частоты повторяемости явлений какой-либо группы изображаются в виде кривой, приведенной на рис. 6, офицер информации может с полным основанием считать, что фактически он изучал не одну, а две различные группы.

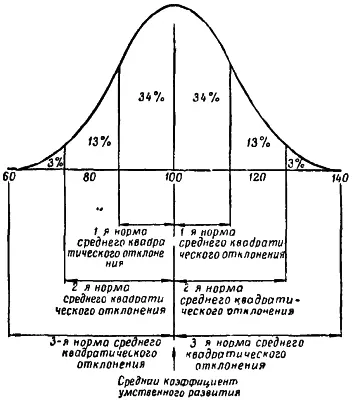
Офицер информации, познакомившись с теорией вероятностей, поймет, что при изучении фактического материала можно извлечь ценную для разведки информацию с помощью такого «параметра», как среднее квадратичное отклонение. Он поймет также, что извлечь пользу из большого количества цифр, например из тысячи цифр, едва ли удастся, если не применить какой-либо обобщающий показатель — параметр. Помимо параметров, служащих для определения степени дисперсии, имеются параметры, характеризующие срединную тенденцию повторяемости величин данной группы. Самыми важными параметрами такого рода являются среднее арифметическое значение, медиана и мода. Все эти параметры иногда объединяют под общим названием «среднее значение». Эта категория является довольно любопытной В среднем значении получает выражение «лучшее из худшего и худшее из лучшего».

Руководствуясь приобретенным ранее" опытом, офицер информации, однако, никогда не принимает за чистую монету поверхностные рассуждения, основанные на средних значениях. В отчетах компаний часто можно встретить следующие заявления:

«Круг акционеров нашей компании весьма широк. Каждый акционер в среднем имеет 100 акций». У многих создается впечатление, что очень большое количество акционеров имеет примерно по сто акций каждый. Приведенное выше заявление обычно делается со специальной целью создать такое впечатление. В действительности подавляющая масса акций может находиться в руках весьма узкой группы акционеров. Вместе с тем правление компании могло провозгласить о своем намерении превратить рабочих и служащих в собственников компании и продать тысячам рабочих и служащих по 5—25 акций каждому. В результате акции могут распределяться следующим образом:

Директор А……………….. 40 000 акций

Директор Б……………….. 25000 акций

Директор В……………….. 20 000 акций

500 рабочих и служащих (по 20 акций у каждого) 10000 акций

500 рабочих и служащих (по 10 акций у каждого) 5 000 акций

1003 акционера владеют…………..100 000 акций

В среднем каждый акционер имеет 99,7 акций.

Разведчик, знакомый с теорией вероятностей, понимает, что медиана или мода лучше выражают срединную тенденцию повторяемости большого количества величин, чем среднее арифметическое значение.

Пожалуй, нагляднее всего сравнительная характеристика среднего значения, медианы и моды дана на схеме в книге Хаффа [73], воспроизведенной на рис. 7.

Разведчик, мыслящий с учетом теории вероятностей, понимает, что обычно отдельные величины группируются вокруг определенного среднего значения и по мере удаления от этого среднего значения дисперсия все более и более увеличивается. Он понимает, что величины, наиболее удаленные от среднего значения, могут существенным образом отличаться от основной массы величин данной группы. В каждом конкретном случае он четко указывает, что его интересует прежде всего основная масса величин или крайние для данной группы величины.

Например, разрабатывая курс лекций для студентов, не следует ориентироваться на самых способных или самых слабых студентов. Лекции, которые могут усвоить самые слабые из 200 студентов первого курса, покажутся совершенно неудовлетворительными студентам со средними способностями, составляющими 90 процентов. Точно так же лекции, которые могут заинтересовать двух-трех наиболее способных студентов, не будут усвоены основной массой студентов.

Напротив, при проектировании моста мы исходим из учета максимальной нагрузки. Мост может провалиться под тяжестью максимальной, а не средней нагрузки.

Офицер информации, знакомый с теорией вероятностей и учитывающий широкую дисперсию внутри данной группы величин, будь то рост людей, дневная температура или точность артиллерийского огня, ясно представляет себе, что, отобрав десять величин из ста, он может случайно столкнуться с крайними или средними для данной группы показателями, например с самым высоким, самым низким или средним ростом людей изучаемой группы Такой разведчик обычно не делает окончательных выводов на основании изучения небольшой выборки без дополнительной работы над проблемой. Он знает, что в информационной работе многие выводы приходится делать на основе выборочного материала. Математическая статистика учит его, каким образом извлекать максимальную пользу из имеющихся выборок, допуская при этом минимум ошибок. Чтобы понимать все это, ему не требуется знать высшую математику.

Офицер информации знает, что внутри неоднородной группы величин можно обнаружить несколько величин, далеко отстоящих в обоих направлениях от среднего для данной группы показателя. Например, среди группы студентов могут встретиться один-два чрезвычайно способных или крайне тупых студента. Из большого количества артиллерийских снарядов, выпущенных по одной цели, один или два без всякой видимой причины упадут с большим перелетом или недолетом В любой политической организации, религиозном или ином движении можно обнаружить небольшое количество фанатиков, взгляды которых все считают слишком крайними и поэтому неразумными. Можно сказать, что нормальным является такое положение, когда несколько процентов крайних для данной группы величин являются анормальными для группы в целом.

Степень отклонения крайних величин от среднего для данной группы показателя зависит обычно от трех факторов. Прежде всего она явно зависит от состава данной группы. Допустим, что в США в одном графстве живет 1000 человек в возрасте от 20 до 30 лет Можно предположить, что среди них найдется несколько человек с низким коэффициентом умственного развития. Однако, если взять 1000 человек такого же возраста, получивших недавно степень доктора философии, среди них вы, конечно, не обнаружите такого отклонения от среднего коэффициента умственного развития.