Вернер Гильде - Зеркальный мир

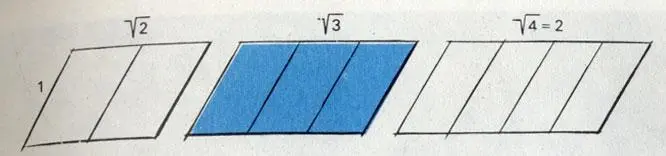
Параллелограммы с соотношением сторон 1 :√ 2, 1 :√ 3 и т. д. можно разделить на две, три и соответственно более частей, так что у новых полученных подобных фигур соотношение сторон сохранится первоначальным

Тот, кто имеет дело с бумагой, знает, что существуют еще два других ряда - для суперобложек и прочих целей. Ряд В начинается с 1414:1000 = 1,414 и ряд С - с 1297:917 = 1,414...

Книга, которую вы читаете (и, хотелось бы надеяться, не без интереса), имеет формат 260Х200 мм, а 260:200 = 1,3.

Конечно, вы обратили внимание, что формат бумаги здесь обозначен не совсем так, как принято: не через произведение сторон, а через их отношение, но мы позволили себе это для большей наглядности.

Мы могли бы сказать, что расчет формата бумаги, отвечающего стандарту, производится путем повторного деления листа с соотношением сторон 1:√ 2, начиная с формата 917Х1297 мм. Но правильнее будет другое определение: стандартный расчет бумаги производится путем пропорционального увеличения листа с соотношением сторон 1:√ 2, последовательно начиная с формата 52Х74 мм. В обоих случаях следовало бы сделать оговорку, что при делении (или умножении) всякий раз берется сторона с относительной длиной √ 2.

В старину подобные трапеции выкладывались по углам наборных полов; каждая составная часть в них подобна целой фигуре

Вспомним, что прямоугольник является лишь частным случаем параллелограмма и что параллелограмм с соотношением сторон 1:√ 2, равно как и прямоугольный равнобедренный треугольник, можно разделить на две уменьшенные копии.

Параллелограмм, одна из сторон которого равняется √ 3, можно разделить на 3 уменьшенные подобные части. В общей форме: параллелограмм с соотношением сторон 1:√ n можно разделить на n одинаковых подобных частей.

Существует еще множество фигур, имеющих самые различные варианты разделения. Мы же рассмотрим еще один мотив, который иногда выкладывали на старинных кафельных полах по углам. Это трапеции, которые зеркальное отражение превращает в цельный мотив узора. Здесь снова возникает «отражение». Значит, в таких узорах допустимы комбинации плоских фигур, которые нельзя путем поворота или вращения совместить друг с другом, то есть «левые» и «правые».

Как уложить бруски или кирпичи, чтобы конструкция не имела сквозных 'швов'

Приведенный здесь рисунок подводит нас к делениям без нарушения сплошности. Если при уменьшении формата бумаги поверхность фигуры пересекал разрыв (складка или черта), то в нашем главном узоре существуют линии, которые не продолжаются, а упираются в другие линии. Иногда особенно желательно полностью избежать деления с разрывами. Скажем, хотелось бы, чтобы стена кирпичного дома не имела шва, пересекающего всю стену сверху донизу. Инструкции по сварке барабанов котлов и нефтяных труб большого диаметра запрещают соприкосновение двух продольных и двух поперечных швов. В каждый поперечный или круговой шов может упираться лишь один продольный шов одного направления. Продольный шов другого направления должен быть непременно смещен в сторону. Благодаря этому разрывы в продольном шве будут распространяться только до следующего поперечного шва.

Теперь вы, наверное, уже догадались, какая предлагается вам задача: соберите из стандартных деталей (кирпичей, паркетин или листов жести) изображенную здесь поверхность, не нарушая ее сплошности.

ЛЕГЕНДЫ РУДОКОПОВ

В старину рудокопы были людьми сугубо практическими. Они не забивали себе голову названиями всевозможных горных пород, которые встречали в штольне, а просто делили эти породы и минералы на полезные и бесполезные, ненужные. Нужные они извлекали из недр, из них плавили медь, свинец, серебро и другие металлы, а ненужные сваливали в отвалы.

Для полезных (на их взгляд) минералов они подыскивали наглядные и запоминающиеся имена. Можно никогда не видеть копьевидного колчедана, но без особого труда представить его себе по названию. Не сложнее по названию отличить красный железняк от бурого железняка.

Для бесполезных камней (как уже было сказано - на их взгляд) горняки нередко находили названия в преданиях и легендах. Так, например, произошло название руды кобальтовый блеск. Кобальтовые руды похожи на серебряные и при добыче иногда принимались за них. Когда из такой руды не удавалось выплавить серебро, считалось, что она заколдована горными духами - кобольдами.

Тяжелый шпат (барит). Рудокопы в стариых выбирали названия для минералов по внешним признакам. Тот, кто однажды взвесил на руке этот минерал и всмотрелся в форму его кристаллов, не забудет его названия

Когда же минералогия превратилась в науку, было открыто великое множество пород и минералов. И при этом все чаще возникали трудности с изобретением для них наименований. Новые минералы часто называли по месту находки (ильменит - в Ильменских горах) или в честь знаменитого человека (гетит - в честь Гете) или же давали ему греческое или латинское название.

Музеи пополнялись грандиозными коллекциями камней, которые становились уже необозримыми. Не слишком помогали и химические анализы, потому что многие вещества одного и того же состава образуют подчас кристаллы совершенно различного облика. Достаточно вспомнить хотя бы снежинки.

Существуют тысячи различных узоров снежинок

В 1850 г. французский физик Огюст Браве (1811-1863) выдвинул геометрический принцип классификации кристаллов, основанный на их внутреннем строении/По мнению Браве, мельчайший, бесконечно повторяющийся мотив узора и есть определяющий, решающий признак для классификации кристаллических веществ. Браве представлял себе в основе кристаллического вещества крошечную элементарную частицу кристалла. Сегодня со школьной скамьи мы знаем, что мир состоит из мельчайших частиц - атомов и молекул. Но Браве оперировал в своих представлениях крошечным «кирпичиком» кристалла и исследовал, каковы могли быть у него углы между ребрами и в каких соотношениях его стороны могли находиться между собой ( Для большей наглядности автор упрощает историю вывода решеток Браве. Предшественник Браве - французский кристаллограф Р. Ж. Гаюи (1743-1822) - действительно представлял себе кристаллы сложенными из элементарных «кирпичиков». О. Браве заменил эти «кирпичики» центрами их тяжести и таким образом перешел от «кирпичной кладки» Гаюи к пространственной решетке. - Прим. ред ).