Мартин Гарднер - Есть идея!

Придуманный Сьюзен метод действительно приводит к простому и эффективному алгоритму для определения числа кратчайших путей, ведущих от ее дома к школе. Если бы Сьюзен попыталась вычертить все пути, чтобы затем пересчитать их, то решение оказалось бы весьма громоздким, а при большом числе улиц просто необозримым. Вы сможете лучше оценить эффективность предложенного Сьюзен алгоритма, если вычертите все 13 путей.

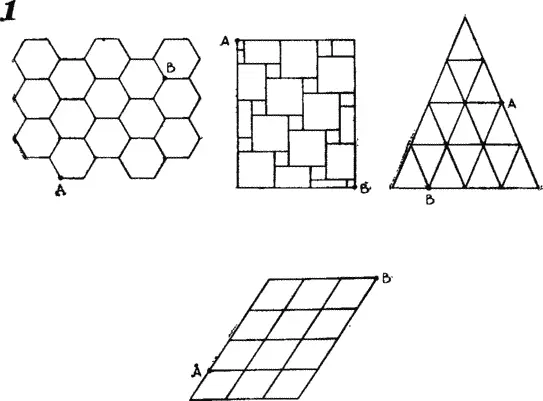
Чтобы проверить, насколько глубоко вы усвоили алгоритмы Сьюзен, попробуйте нарисовать сети улиц, имеющие другие конфигурации, и подсчитать число кратчайших путей, ведущих из точки А в точку В. Четыре задачи этого типа представлены на рис. 1 . Решать их можно по-разному, например, воспользоваться комбинаторными формулами, но все методы несколько сложнее алгоритма Сьюзен.

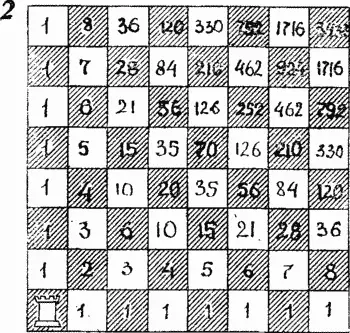
Чему равно число кратчайших путей, по которым ладья может перейти из одного углового поля на шахматной доске в другое, диагонально противоположное? Эта задача легко решается, если каждому полю на шахматной доске приписать по числу так же, как Сьюзен приписывала числа перекресткам на карте города. Ладья ходит только по горизонтали и вертикали. Следовательно, кратчайший путь из любой клетки в любую другую состоит в преодолении разделяющего клетки расстояния по горизонтали и по вертикали. Если числа расставлены верно (см. рис. 2 ), то они указывают число кратчайших путей, ведущих из нижнего угла в любое поле. Например, поле в правом верхнем углу помечено числом 3432. Следовательно, ладья может перейти с поля, стоящего в левом нижнем углу доски на диагонально противоположное поле 3432 кратчайшими путями.

Разрезав шахматную доску по диагонали и повернув половину, мы получим треугольник, изображенный на рис. 3 . Числа, стоящие в клетках любого ряда, указывают число кратчайших путей, ведущих в них из самой верхней клетки. Расставленные в клетках числа образуют знаменитый арифметический треугольник Паскаля, и это не удивительно: алгоритм для подсчета числа кратчайших путей, ведущих от вершины, в точности совпадает с процедурой построения треугольника Паскаля. Этот изоморфизм позволяет считать исходную головоломку прологом к изучению необычайно разнообразных и красивых свойств треугольника Паскаля.

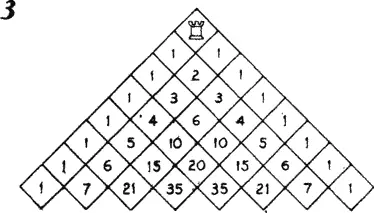
Треугольник Паскаля позволяет находить биномиальные коэффициенты (то есть коэффициенты при любом члене разложения ( a + b ) n , где n — любое целое число) и решения многих задач элементарной теории вероятностей. Заметим, что на рис. 3 число кратчайших путей, ведущих из вершины треугольника в самую левую или самую правую клетку нижнего ряда, равно 1 и что по мере приближения к середине ряда число кратчайших путей возрастает. Возможно, вам случалось видеть одно из устройств, действие которых основано на свойствах треугольника Паскаля: по наклонной доске, в которую в шахматном порядке вбиты колышки, скатываются шарики и скапливаются в отсеках под колышками нижнего ряда. Распределение шариков имеет форму колоколообразной кривой, а число шариков в каждом отсеке пропорционально соответствующему биномиальному коэффициенту, потому что число кратчайших путей, ведущих в каждый отсек, в точности совпадает с определенным биномиальным коэффициентом.

Алгоритм, предложенный Сьюзен, как нетрудно понять, остается в силе и для трехмерных сетей, в которых ячейки («кварталы») имеют форму прямоугольных параллелепипедов. Представьте себе куб с длиной ребра 3 единицы, разделенный на 27 единичных кубов. Будем считать его пространственной шахматной доской и в угловую «клетку» поместим ладью, которая может двигаться параллельно любому из ребер куба. Сколькими способами ладью можно перевести кратчайшим путем в клетку, расположенную на другом конце диагонали куба?

В одном родильном доме по чьему-то недосмотру перепутали карточки с именами 4 младенцев. У двух детей оказались их карточки, а карточки остальных двух малюток были разложены неправильно.

Сколько существует различных вариантов путаницы?

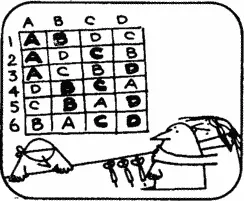
Подсчитать число вариантов совсем нетрудно, если составить таблицу. Оказывается, что карточки с именами 2 детей из 4 можно перепутать лишь 6 различными способами.

Предположим теперь, что после того, как карточки перепутали, у трех детей оказались карточки с их именами, а одному младенцу досталась карточка с чужим именем. Сколько вариантов путаницы существует в этом случае?

Как бы вы стали решать эту задачу? Составили бы таблицу? А может быть, у вас есть идея, как решить эту задачу проще?

Многим кажется, что ответить на вопрос задачи довольно трудно. Те, кто так думает, ошибочно полагают, будто перепутать карточки так, чтобы 3 младенцам из 4 достались карточки с их именами, можно многими способами. Но стоит лишь обратиться к принципу «птичка в клетке» и сформулировать задачу несколько иначе, как ответ сразу становится очевидным. Предположим, что перед нами 4 клетки и на каждой из них укреплена карточка с названием одного из 4 предметов. Если 3 предмета попали в клетки со своими названиями, то четвертому предмету не остается ничего другого, как попасть в клетку, к которой прикреплена карточка с его названием. Таким образом, мы имеем дело лишь с одним вариантом: каждый из 4 предметов оказывается в своей клетке.

Во многих книгах по занимательной математике встречается следующая задача, в которой речь идет лишь о 3 предметах. На столе расставлены 3 закрытые коробки. В одной из них находятся 2 монеты по 5 центов, в другой — 2 монеты по 10 центов и в третьей — 1 пятицентовая и 1 десятицентовая монета. На крышках коробок написано: 10 центов; 15 центов и 20 центов, но ни одна из надписей не соответствует содержимому коробки. Предположим, что из коробки с надписью «15 центов» (напомним, что надпись не соответствует содержимому коробки) извлекли 1 монету и положили на стол перед коробкой. Можно ли, взглянув на эту монету, сказать, какие монеты находятся в каждой из 3 коробок?