Георгий Гамов - Приключения Мистера Томпкинса

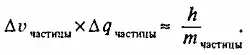
(6)

Для тел, с которыми нам обычно приходится иметь дело, неопределенность (6) до смешного мала. Так, в случае легкой пылинки с массой 0,0000001 г и положение, и скорость могут быть измерены с точностью 0,00000001 %! Однако в случае электрона (с массой 10^-27 г) произведение (дельта)u * (дельта)q достигает величины порядка 100. Внутри атома скорость электрона необходимо определять по крайней мере в пределах +-10^8 см/с, в противном случае электрон окажется вне атома. Это дает для положения электрона неопределенность 10^8 см, т. е. неопределенность, совпадающую с полными размерами атома. Таким образом, «орбита» электрона в атоме расплывается до такой степени, что «толщина» траектории становится равной ее «радиусу» — электрон оказывается одновременно всюду вокруг ядра .

На протяжении последних двадцати минут я пытался нарисовать вам картину разрушительных последствий нашей критики классических представлений о движении. Изящные и четко определенные классические понятия оказываются вдребезги разбитыми и уступают место тому, что я назвал бы бесформенной размазней. Естественно, вы можете спросить меня, как физики собираются описывать какие-нибудь явления, если квантовый мир буквально захлестывают волны океана неопределенности. Ответ состоит в том, что до сих пор нам удалось лишь разрушить классические понятия, но мы еще не пришли к точной формулировке новых понятий.

Займемся этим теперь. Ясно, что мы не можем, вообще говоря, определить положение материальной частицы с помощью материальной точки, а траекторию ее движения — с помощью математической линии, поскольку в квантовом мире все объекты расплываются. Нам необходимо обратиться к другим методам описания, дающим, так сказать, «плотность размазни» в различных точках пространства. Математически это означает, что мы используем непрерывные функции (такие как, например, в гидромеханике), а физически требует, чтобы при описании квантового мира мы употребляли такие обороты речи, как «этот объект в основном находится здесь, частично там и даже вон там» или «эта монета на 75% находится в моем кармане и на 25% — в вашем». Я понимаю, что такие утверждения кажутся вам дикими, но в нашей повседневной жизни из-за малости квантовой постоянной в них нет надобности. Но если вы вознамеритесь изучать атомную физику, то я настоятельно рекомендую вам предварительно привыкнуть к такого рода выражениям.

Считаю своим долгом предостеречь вас от ошибочного представления о том, будто функция, описывающая «плотность пребывания» объекта в различных точках пространства, обладает физической реальностью в нашем обычном трехмерном пространстве. Действительно, если мы описываем поведение, например, двух частиц, то нам необходимо ответить на вопрос, находится ли одна частица в одном месте и, одновременно, вторая частица в другом месте. Для этого нам необходима функция шести переменных (координат двух частиц), которую невозможно «локализовать» в трехмерном пространстве. Для описания более сложных систем нам понадобились бы функции еще большего числа переменных. В этом смысле «квантово-механическая функция» аналогична «потенциальной функции», или «потенциалу», системы частиц в классической механике или «энтропии» системы в статистической механике: она только описывает движение и позволяет нам предсказывать результат любого конкретного движения при данных условиях. Физическая реальность остается за частицами, движение которых мы описываем.

Функция, которая описывает, какая «доля» частицы или системы частиц присутствует в различных местах пространства, требует специального математического обозначения. Следуя Эрвину Шредингеру, который первым написал уравнение, определяющее поведение такой функции, ее стали обозначать

.

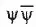
Я не стану сейчас вдаваться в детали математического вывода фундаментального уравнения Шредингера. Хочу лишь обратить ваше внимание на требования, которые привели к его выводу. Самое важное из этих требований весьма необычно: уравнение должно быть записано в таком виде , чтобы функция, описывающая движение материальных частиц, обладала всеми свойствами волн ы .

На необходимость наделить движение материальных частиц волновыми свойствами впервые указал французский физик Луи де Бройль на основе своих теоретических исследований строения атома. В последующие годы волновые свойства движения материальных частиц были надежно подтверждены многочисленными экспериментами, продемонстрировавшими такие явления, как дифракция пучка электронов при прохождении через малое отверстие и интерференционные явления , происходящие даже с такими сравнительно большими и сложными частицами, как молекулы.

Экспериментально установленные волновые свойства материальных частиц были совершенно непонятны с точки зрения классических представлений о движении, и де Бройль был вынужден принять весьма необычную (чтобы не сказать неестественную) точку зрения: по де Бройлю, все частицы «сопровождаются» определенными волнами, которые, так сказать, «направляют» их движения.

Но как только мы отказываемся от классических понятий и переходим к описанию движения с помощью непрерывных функций, требование о волновом характере становится гораздо более понятным. Оно просто утверждает, что распространение нашей

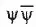
—функции аналогично (например) нераспространению тепла сквозь стенку, нагреваемую с одной стороны, а распространению сквозь ту же самую стенку механической деформации (звука). Математически это означает, что мы ищем уравнение определенного (а не ограниченного) вида. Это фундаментальное условие вместе с дополнительным требованием, чтобы наши уравнения, если их применять к частицам большой массы, переходили в уравнения классической механики, поскольку квантовые эффекты для таких частиц становятся пренебрежимо слабыми, практически сводят проблему вывода уравнения к чисто математическому упражнению.

Если вас интересует, как выглядит окончательный ответ — фундаментальное уравнение Шредингера, то я могу выписать его. Вот оно:

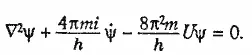
(7)

Здесь U означает потенциал сил, действующих на нашу частицу (с массой m), и порождает определенное решение задачи о движении частицы при любом заданном распределении силы. «Волновое уравнение Шредингера» (так принято называть выведенное Шредингером фундаментальное уравнение) позволило физикам в последующие сорок лет его существования построить наиболее полную и логически непротиворечивую картину явлений, происходящих в мире атомов.