Георгий Гамов - Приключения Мистера Томпкинса

— Не-ет, — задумчиво протянул мистер Томпкинс, и кондуктор пошел своей дорогой, качая головой.

Вдруг чья-то тяжелая рука опустилась на плечо мистера Томпкинса, и, очнувшись, он обнаружил, что сидит не в вокзальном буфете, а на скамье в той самой университетской аудитории, где он слушал лекцию профессора. Свет уже был потушен, и аудитория опустела. Разбудивший его университетский служитель мягко заметил:

— Мы закрываемся, сэр! Если хотите спать, ступайте лучше к себе домой.

Мистер Томпкинс встал и направился к выходу.

Леди и джентльмены!

Человеческий разум сформировал определенные представления о пространстве и времени как о вместилище или арене, на которой происходят различные события. Эти представления без особых изменений передавались из поколения в поколение, а со времени зарождения точных наук были включены в самые основы математического описания окружающего нас мира. Великий Ньютон, по-видимому, первым дал четкую формулировку классических понятий пространства и времени, написав в своих «Математических началах»:

«Абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным» и «Абсолютное , истинное математическое врем я само по себе и по самой своей сущности , без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью» [2].

— Убеждение в абсолютной правильности этих классических представлений о пространстве и времени было столь сильным, что философы часто считали их априорными и ни одному ученому-естествоиспытателю даже в голову не приходило усомниться в них. Однако в начале XX века стало ясно, что ряд результатов, полученных с помощью чувствительных и тонких методов экспериментальной физики, приводят к противоречиям, если их интерпретировать в рамках классических представлений о пространстве и времени. Это обстоятельство привело одного из величайших современных физиков Альберта Эйнштейна к революционной идее: не существует никаких причин, кроме традиции, по которым классические представления о пространстве и времени следовало бы считать абсолютно правильными; в эти понятия можно и должно вносить изменения, чтобы они соответствовали нашему новому, более точному опыту. Действительно, классические понятия пространства и времени были сформулированы на основе человеческого опыта, почерпнутого из повседневной жизни. Нужно ли удивляться, что тонкие и точные современные методы наблюдения, основанные на использовании высокоразвитой экспериментальной техники, указывают на то, что старые понятия пространства и времени слишком грубы, неточны и могли использоваться в повседневной жизни и на более ранних стадиях развития физики только потому, что их отклонения от правильных понятий достаточно малы. Не следует удивляться и тому, что расширение области исследований современной науки рано или поздно должно было привести нас в такие области, где эти отклонения весьма велики и классические понятия вообще не применимы.

Самым важным экспериментальным результатом, приведшим к коренному пересмотру наших классических представлений, стало открытие того факта, что скорость света в пустоте представляет собой верхний предел всех возможных физических скоростей. Такой важный и неожиданный вывод был сделан главным образом на основании экспериментов американского физика Майкельсона, который в конце прошлого века предпринял попытку наблюдать влияние движения Земли на скорость распространения света и к своему великому удивлению и к удивлению всего научного мира обнаружил, что никаких эффектов, свидетельствующих о влиянии скорости движения Земли на скорость света, не существует и что скорость света в пустоте оказывается всегда одной и той же, независимо от системы, в которой производится измерение, или от движения источника, испускающего свет. Нет необходимости объяснять, почему такой результат весьма необычен и противоречит нашим фундаментальным представлениям о движении. Действительно, если какой-то объект быстро движется в пространстве, а вы движетесь навстречу ему, то движущийся объект столкнется с вами с большей относительной скоростью, равной сумме скоростей объекта и наблюдателя. С другой стороны, если вы удаляетесь от объекта, то он, догнав вас сзади, столкнется с вами с меньшей относительной скоростью, равной разности скоростей.

Например, если вы движетесь, скажем, едете в автомашине, навстречу распространяющемуся в воздухе звуку, то измеренная из машины скорость звука будет больше на величину, равную скорости, развиваемой вашей машиной, или, соответственно, меньше, если звук догоняет вас. Мы называем это теоремой сложения скоростей . Всегда считалось, что эта теорема самоочевидна.

Однако, как показали самые тщательные эксперименты, в случае света теорема сложения скоростей нарушается: скорость света в пустоте всегда остается одной и той же и равна 300000 км/с (скорость света принято обозначать строчной латинской буквой с) независимо от того, как быстро движется наблюдатель.

— Все это хорошо, — скажете вы, — но разве нельзя построить сверхсветовую скорость, складывая несколько меньших, физически достижимых скоростей?

Можем же мы представить себе движущийся очень быстро (например, со скоростью, равной 3/4 скорости света) поезд и бродягу, бегущего по крышам вагонов также со скоростью, равной 3/4 скорости света.

По теореме сложения скоростей, общая скорость бродяги была бы равна полутора скоростям света, и бродяга мог бы обогнать свет, испускаемый сигнальным фонарем. Однако истина состоит в том, что, поскольку постоянство скорости света есть экспериментальный факт, результирующая скорость в нашем случае должна быть меньше, чем мы ожидаем, — она не может превосходить критического значения с. Таким образом, мы приходим к выводу о том, что и при меньших скоростях классическая теорема сложения скоростей должна быть неверна.

Математический анализ проблемы, в который я не хочу здесь вдаваться, приводит к очень простой новой формуле для вычисления результирующей скорости двух складываемых движений.

Если u1 и u2 — две подлежащие сложению скорости, то результирующая скорость оказывается равной

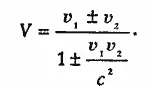
(1)

Вы видите из этой формулы, что если обе подлежащие сложению скорости малы (я имею в виду «малы по сравнению со скоростью света»), то вторым членом в знаменателе формулы (1) можно пренебречь по сравнению с единицей и вы получаете классическую теорему сложения скоростей. Если же скорости u1, и u2 не малы, то результат будет несколько меньше арифметической суммы скоростей. Так, в нашем примере с бродягой, бегущим по крышам вагонов мчащегося поезда, u1 = (3/4)c и u2 = (3/4)c и наша формула позволяет найти результирующую скорость F = (24/25) с, которая, как и складываемые скорости, меньше скорости света.