Дмитрий Черкасов - Строение и законы Вселенной

В обеих задачах ставится очень важный практический вопрос о возможности описаний и вычисления многомерной поверхности, что необходимо для расчетов пространственных взаимодействий, например, химических реакций, тепло- и массопереноса и т. д. Здесь ответ на вопрос определяется рациональным выбором системы координат. Обычно используются прямоугольные системы, а полярные существенно упрощаются, что делает неизбежными ошибки даже при наиболее простых работах на поверхности геоида (Земли). Применение же более сложных систем неевклидовой геометрии, четырехмерных и более пространств либо сопровождается значительным увеличением объемов расчетов, либо ведет к многозначности ответа, либо происходит и то и другое вместе.

Предложения о сведении любой структуры к набору достаточно простых (в смысле математического описания) геометрических фигур являются перспективными. Но! По формальным признакам, что осложняет перенос решений в ЭВМ, возникают особые точки ; где решения неоднозначны.

Предложенная задача Ходжи и является одной из попыток как-то скорректировать неоднозначность решения. При ее решении представляется наиболее разумным применить аналого-цифровой подход.

Известная нам Вселенная в своей основе состоит из полевых структур, в частности атомных и субатомных, образующих и так называемую материю-субстрат с более или менее определенными границами. Каждая частица имеет границу объема, далее которой она перестает быть сама собой. Определение этой границы является аналоговой операцией, констатирующей, где происходит переход количества в качество. Далее происходит просто цифровой счет. Это и есть наиболее общее решение задачи. Автор считает, что, скоординировав работу известных ему специалистов и финансируя эту работу так, как она того заслуживает, и посвятив ей лет 5–6, он мог бы получить как одно из решений этой задачи, так и несколько сопутствующих решений задач, здесь не приведенных по определению эталонных значений и систем координат, но предпочитает оставить эту рутинную (в хорошем смысле слова) работу коллективам математиков и физиков. К тому же примерная стоимость экспериментов и расчетов на 2 порядка превысит размер объявленной премии.

Здесь важно определить уровень размерности, где указанный цифровой счет производится. Например там, где присутствует гладкая с точки зрения технических целей поверхность, при приближении измерительного эталона к размеру атомных частиц поверхность становится достаточно сложной и не совсем ровной. Значит, здесь следует решить более общую задачу, такую как выбор или создание системы координат, назначение эталона единицы величины и «сшивание» решений в особых точках.

Задачи типа определения, где какая поверхность у кольца Мебиуса, или геометрической фантазии Эшера очень интересны, познавательны и стимулируют воображение на создание оригинальных идей и решений. Однако здесь допускается одна маленькая хитрость — не указывается, в какой системе координат все это существует, так как в этом случае вся таинственность пропадает.

Если мы, например, рассмотрим кольцо Мёбиуса во внешней трехмерной координатной системе с фиксированным положением нуля отсчета и «+» или «-», то внешним или внутренним будет проекция поверхности на соответствующую плоскость. И всё! Это дает абсолютно однозначное решение. Если положение кольца изменилось, соответственно изменятся и положения проекций. Если система координат связана с поверхностью кольца, то там вообще сложная, но двухмерная задачка. Все зависит от формы и полноты задания граничных условий и даже от более точного определения, что считать наружной, а что — внутренней стороной.

Гипотеза Пуанкаре о соразмерности топологически разных объектов также является очень важной практической задачей реальной человеческой деятельности. Например, как из материала поверхности шара скроить тороид, при этом выполнив какой-то критерий вроде одного разреза или равенства площадей поверхностей. Однако перевод решения в N-мерное (более трех) пространство делает эту задачу более подходящей для развития математической логики, а не для решения практических задач, реализация которых все равно происходит в трехмерном мире.

В следующей задаче производится попытка связать законы микро- и макромиров на основе системы непротиворечивых уравнений.

Сразу отметим, что в поставленной коллективом ученых из Clay Mathematics Institute задаче отсутствует математическая запись уравнения, которое должно быть уточнено или расширено (этим, кстати говоря, грешат многие заказчики научных и технологических решений, не затрудняющие себя определением граничных условий задачи, тем самым-как бы «размывая» цель исследования и затрудняя поиск приемлемого ответа). Э го также дает возможность недобросовестному заказчику отказать в выдаче обещанного вознаграждения.

В каноническом виде уравнение Навье — Стокса определяет движение несжимаемой вязкой жидкости и записывается в виде

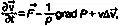
где v — вектор скорости; t — время; F — вектор напряженности массовых сил; ρ — плотность среды; Р — гидродинамическое давление; n — кинематическая вязкость.

В соответствии с определением в исследуемой жидкости должно выполняться условие несжимаемости

divV = 0

соответствующее определению «ньютоновской жидкости», и условие распределения напряжений, соответствующее определению «ньютоновской жидкости».

При движении потоков вблизи твердых границ на неподвижных границах за счет прилипания частиц выполняется условие прилипания

v=o,

а на подвижных границах

V = V t

где V t— скорость точек твердой поверхности.

Таким образом, получается замкнутая система уравнений, позволяющая при определенных граничных условиях вычислить сопротивление в канале или для тел, движущихся в вязкой жидкости. Ограничениями, влияющими на точность решения, являются:

• узкие рамки исследуемого диапазона скоростей: например, для газов V ≤ 0,1÷0,2 V звука, так как далее необходимо учитывать сжимаемость;

• нелинейные геометрические эффекты — вихревые системы за движущимся или обтекаемым телом, геометрические характеристики которого определяются взаимозависимыми характеристиками, в первую очередь, скоростями в потоке;

• нелинейные динамические эффекты — отрыв и перенос вихрей, изменение температуры, рассеивание энергии в потоке и на границах;

• нелинейные физические эффекты — изменения физических и химических свойств жидкостей и газов (коэффициентов взаимодействия, фазовых состояний, растворимости и т. д.).