Стаффорд Бир - Мозг фирмы

Представим себе такой простой цифровой пример: пусть функция преобразования удваивает входную величину. Пусть в данный момент значение на входе равно 3, тогда на входе будет 6, а 6 и есть то, что мы хотим. Представим теперь, что по неизвестной нам заранее причине значение на выходе внезапно стало равным 8. Тогда отклонение на 2 будет воспринято как изменение значения на выходе, а отсюда следует, что значение на входе по той или иной причине по своему эффекту стало равно 4. Цепь обратной связи воспримет как свою входную величину отклонение выходной величины (на 2 единицы) и теперь должна сработать при таком его значении. Если она просто направит обратно отклонение в 2 единицы как поправку на вход в систему, то теперь при его, как мы помним, значении, равном 4, на входе останется только 2. Функция преобразования его удвоит, и новое значение на выходе станет равным 4 вместо 6. Ясно, что цепь обратной связи нуждается в своей собственной функции преобразования, которая снизит первичное отклонение выходной величины с 2 до 1 и заставит первичное отклонение на входе снизиться на это значение. Тогда выходное значение системы возвратится к требуемой цифре б, поскольку входная величина теперь исправлена на 3.

Этот пример хорошо демонстрирует механизм действия отрицательной обратной связи, исправляющей ошибку, но он с дефектом.

Мы заморозили систему, чтобы рассмотреть фактические показатели, а затем позволили ей работать снова на конечном интервале времени, необходимом для срабатывания обратной связи. Однако причиной всех неприятностей является неожиданное изменение входного сигнала, и, вероятнее всего, он изменится снова к моменту проведения корректирующих действий. Тогда то, что произойдет за время отклонения и введения в систему обратной связи, сложнее, чем просто изменение на обратное значение первичной функции преобразования. Если бы это была единичная операция, то легко было бы видеть, что систематическое изменение входной величины, которое происходит в фазе с временным циклом обратной связи, будет не подавлено, а усилено. Наш механизм обратной связи обнаружит первичное отклонение+ 2, и снижение входной величины на единицу последует точно в момент, когда на входе будет импульс, приводящий в результате к отклонению на -2. Иначе говоря, на входе останется величина 2, что генерирует 4 скорее, чем 6. Тут начнет действовать обратная связь, считывающая первое (позитивное) отклонение, и снизит входное значение с 2 до 1. Теперь на выходе останется 2 вместо 6, что еще хуже.

Из этого следует, что в цепи обратной связи должна быть обеспечена своя собственная функция преобразования, которая может быть записана как F ( p ), и она должна быть умно реализована, чтобы скорее подавлять, чем усиливать флуктуации на входе. Допустим, что так или иначе это может быть сделано и мы получим тот впечатляющий результат, которого добиваемся — саморегулирующий механизм, в основе действия которого лежит не причина нарушения, а производимый ею эффект. Дело в том, что причиной отклонения может быть или изменение температуры ( а в системе не предусмотрено ее обнаружение), или нарушение соединения (которое не предполагалось), или отказ в другой системе, генерирующей входную величину для данной системы (о которой система "ничего не знает"). Для нас важно, чтобы управление осуществлялось независимо от причины нарушения.

Чтобы уяснить различие между первичной функцией преобразования f ( p ) и новой функцией F ( p ), мы должны обратиться к первичной сети и сети обратной связи, которые управляются этими двумя функциями соответственно. "Сеть"— по-прежнему подходящий для нас термин, поскольку реальные системы значительно сложнее простых из числа здесь рассмотренных, в которых можно разглядеть единичные линии и цепи. "Сеть" на простом русском языке звучит лучше, чем латинское "ретикулум", как упоминалось ранее, поскольку теперь мы создаем систему со специально приспособленными соединениями. К названию ретикулум будем прибегать, ссылаясь на общие и, возможно, специальные случаи внутренних соединений в том контексте, в каком это слово первоначально было введено.

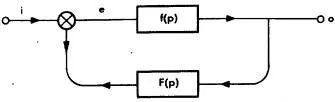
Рис.8

Теперь обратимся к схеме простого сервомеханизма (рис.8) — нам предстоит исследовать характеристики обратной связи на основематематического описания. Это не означает, что мы будем изучать конкретные дифференциальные уравнения — вся дискуссия ограничится элементарными алгебраическими уравнениями, но это надо преодолеть. На вход системы обратной связи подается выходная величина основной системы — о. Выходная величина системы обратной связи есть результат воздействия на величину о функции преобразования системы обратной связи, т.е. oF ( p ). На входе предыдущей системы в результате воздействия обратной связи вместо величины i будет величина е = i+ oF ( p ). их

Если это так, то форма функции преобразования первичной системы изменится. Первоначально мы ее записали как f ( p ) = o / i , но теперь это неверно. На входе основной системы (прямоугольник f ( p )) теперь уже величина не i, а е, представляющая суммарный эффект входной величины i и величины, обусловленной действием обратной связи, oF ( p ).

Поскольку на входе блока f ( p ) величина е, а на выходе о, то f ( p ) = о/е. Чтобы получить функцию преобразования всей системы, мы должны вернуться к основному определению, в котором выходная величина сравнивалась с входной, и записать новую функцию я(р), которая устанавливает правильное соотношение между функциями f ( p ) и F ( p ). Конечно, просто записать 0 (р) =o/i. Но чтобы сделать то, что нам нужно, перепишем уравнение для первой системы f ( p ) и уравнение для е. Тогда получим

o ( р ) = o/i = f (p) / [l-f(p)F(p) ]

Из данного уравнения следует несколько выводов. Во-первых, видно, что обратная связь может стать либо положительной, либо отрицательной.

Рассмотрим произведение функций обратной связи первичной цепи и цепи обратной связи, а именно f ( p ) F ( p ). Предположим, что система не требует коррекции, т.е. функция обратной связи не оказывает никакого влияния. Тогда перемножение функций даст нуль и общая функция преобразования o( p ) будет правильно работать как f ( p ) сама по себе. Если произведение функций будет больше нуля, то знаменатель станет меньше единицы, а общее значение функции больше значения функции преобразования первичной цепи — в итоге получится положительная обратная связь. Если произведение функций станет меньше нуля, то знаменатель станет больше единицы и значение результирующей функции станет меньше значения функции преобразования первичной цепи — получим отрицательную обратную связь. Очевидно, что в одной и той же системе может быть как положительная обратная связь, так и отрицательная, в зависимости от формы переменной, действующей на входе, и сдвига по фазе во взаимодействии этих двух цепей.