Ольга Шиян - Развитие творческого мышления. Работаем по сказке

Если дети согласятся, но объяснений не дадут, педагог спрашивает:

— А как вы думаете, в чем петух самый-самый?

Дети скорее всего скажут, что он лису прогнал — поэтому и самый-самый.

Если вдруг кто-то вспомнит, что именно петух лису прогнал, то этот ответ следует поддержать.

Педагог задает вопрос:

— А кто кого обычно боится — лиса петуха или петух лису?

После того как дети вспомнят, что вообще-то лисы петухов едят, а вовсе не наоборот, спрашивает:

— Так как же вышло, что в нашей сказке лиса петуха испугалась?

Важно, чтобы дети смогли найти объяснение — предложили то качество, которое и позволило петуху прогнать лису. Таким свойством может оказаться хитрость или храбрость. Можно вернуться к тексту сказки и вспомнить, что петух нес косу, да еще угрожал лисе своими красными сапогами — видимо, чтобы напугать.

— А остальные звери придумали что-нибудь, чтобы лису напугать?

Тут опять придется вернуться к сказке, прочитать реплики всех героев, чтобы убедиться, что все, кроме петуха, говорили вполне стандартные слова: «Ступай, лиса, вон», которые на лису не действовали.

Возвращение к решению диалектической задачи при помощи наглядной модели.

Педагог оставляет на доске только картинки с медведем и петухом и спрашивает:

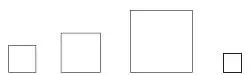
— Так как нам быть — кто же тут самый-самый, кому же должен достаться самый большой квадрат? Медведю или петуху? Кто из них самый-самый?

Стоит еще раз уточнить, почему каждый из них заслуживает самого большого квадрата: медведь — потому что самый большой, а петух — потому что самый храбрый.

Если дети не смогут найти решение, можно показать им боковую часть доски с остальными квадратами и спросить: «Может, эти квадраты нам как-то помогут?»

Если дети предложат квадрат меньшего размера (черный или белый), надо показать, что герои могут обидеться: каждый из них самый-самый, почему же одному большой квадрат, а другому — маленький?

Диалектическое преобразование — решение задачи.

Решением будет предложение оставить для одного из героев большой белый квадрат, а для второго взять самый большой квадрат другого, черного, цвета.

Педагог:

— Так вот оно что: они по-разному самые-самые: медведь самый-самый большой по размеру — его мы обозначим большим белым квадратом. А петух самый-самый по храбрости — его мы обозначим самым большим черным квадратом.

Далее можно сделать те же два шага, что и при работе по сказке «Колобок»: построить наглядную модель сначала по одному основанию (по размеру), а потом — по другому (по храбрости).

На доске остается только медведь, под ним большой белый квадрат.

— Вы говорите, что медведь самый большой по размеру. Давайте тоже расставим по размеру остальных героев, и каждому дадим свой квадратик. Первым заяц встретил собаку. (На доску прикрепляется картинка с собакой.) А какой квадратик ей подойдет?

Проблемно-противоречивый вопрос.

Ловушка может поджидать детей при поиске квадрата для петуха: если ребята дадут ему самый большой белый квадрат, педагог напоминает, что они строят серию по росту.

Необходимо убедиться, что дети правильно понимают, кто каким квадратом по росту обозначен. Например, можно предложить угадать по квадрату героя, или выстроить квадраты-модели в ряд в случайном порядке, а потом предложить прочитать, кто за кем стоит, или поменять квадраты-модели местами и попросить ответить на вопрос: «Кто с кем поменялся? и т. д.

Только после этого педагог переходит к следующему заданию:

— Итак, у нас на доске не просто квадратики, они обозначают героев сказки. А давайте попробуем выстроить наших героев по росту.

Детям может оказаться непросто преодолеть ту последовательность, которая задана сказкой, и выстроить героев от самого маленького к самому большому. Вопрос возникнет относительно квадратика-модели петуха — куда его ставить, в конец ряда или сразу после собаки.

Если прозвучат разные версии, стоит заострить проблемную ситуацию, вызвать детей, предлагающих разные решения, к доске и спросить:

— Вася предлагает поставить квадратик с петухом после собаки, а Петя — в конец. Кто же из них прав? Объясните!

Обоснование противоположных суждений.

— Может, прав Петя — ведь лиса нам в конце сказки встретилась?

— А может, прав Вася — ведь петух меньше остальных зверей, значит, он должен стоять в самом начале?

Решение задачи заключается в том, что обе серии правильные, но выстроены они по разным основаниям — «по сказке» (т. е. «по сюжету») и по размеру. Воспитатель не подсказывает ответ, но помогает каждому ребенку обосновать свою точку зрения.

Решением будет обнаружение разных оснований для сравнения:

— Вася был бы прав, если бы мы выстраивали героев по сказке, но мы-то их выстраиваем по росту!

При подведении итогов можно выстроить разные варианты серий и попросить детей угадать, как серия выстроена, по какому основанию: по росту, по сказке, в обратную сторону по росту и т. п.

Возвращение к проблемно-противоречивой ситуации при помощи наглядной модели.

Педагог ставит большой черный квадрат под картинкой с петухом и спрашивает: «А почему у нас петух получил самый большой квадрат?»

Важно выслушать ответы детей: назовут ли они храбрость или ум как другое основание для сравнения.

Далее педагог предлагает детям подобрать квадрат для обозначения собаки. Скорее всего, эта просьба не вызовет затруднений — для собаки ребята выберут самый маленький черный квадрат (напомним, что размеры животных на картинках отражают их относительные размеры). Если, однако, вдруг собаке будет предложен маленький белый квадрат, педагог останавливает беседу — это значит, дети путают основания — и уточняет:

— Белым цветом мы обозначали разных по росту героев, а сейчас мы о каком качестве говорим?

Педагог предлагает подобрать квадраты, обозначающие храбрость волка и медведя.

Диалектическое преобразование — решение задачи.

Работа должна вестись так же, как по сказке «Колобок»: дети должны открыть, что по храбрости эти герои не отличаются и заслуживают одинаковые квадраты. Педагог выясняет, смогут ли дети совершить перенос и обнаружить в другой сказке принципиально те же структурные отношения: несмотря на различие в видимом качестве (размере), по скрытому (но существенному для сюжета сказки) качеству герои не различаются.