Леонард Сасскинд - Битва при черной дыре. Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики

Лайнландцам понадобилось название для нового направления, и они обозначили его Y. В отличие от Х, вдоль Y нельзя далеко уйти, не вернувшись в исходную точку. Лайнландские математики говорят, что направление Y компактифицировано.

Цилиндр, изображенный выше, получается при добавлении дополнительного свернутого измерения к исходному одномерному миру. Добавление шести дополнительных измерений к миру, в котором уже есть три обычных, выходит далеко за пределы способностей человеческого мозга к визуализации. Физиков и математиков отличает от остальных людей не то, что они мутанты, способные представить себе любое число измерений, а скорее то, что они прошли тяжелую математическую переподготовку, опять же, перепрошивающую сознание, — чтобы научиться «видеть» дополнительные измерения.

Единственное дополнительное измерение не обеспечивает достаточного разнообразия возможностей. Перемещение в свернутом направлении будет подобно движению по кругу без осознания этого. Но уже два дополнительных измерения открывают бесконечное множество новых возможностей. Два измерения могут образовать сферу.

тор (поверхность бублика),

бублик с двумя или тремя дырками,

или даже причудливое пространство, называемое бутылкой Клейна.

Изображение двух дополнительных измерений не составляет больших проблем (мы только что сделали это), но с ростом числа измерений визуализировать их становится все труднее и труднее. К тому моменту когда мы достигнем шести дополнительных измерений, необходимых для теории струн, визуализация без обращения к математике становится безнадежным делом. Особые геометрические пространства, которые струнные теоретики используют для компактификации шести дополнительных измерений, называются многообразиями Калаби — Яу. Их насчитываются миллионы, и среди них нет двух одинаковых. Многообразия Калаби — Яу исключительно сложны, с сотнями шестимерных дырок от бубликов и прочими невообразимыми кренделями. Тем не менее математики создают их изображения, нарезая на слои меньшей размерности, подобно диаграммам вложения [135] См. главу 3. — Примеч. перев. . Вот изображение двумерного среза типичного пространства Калаби — Яу.

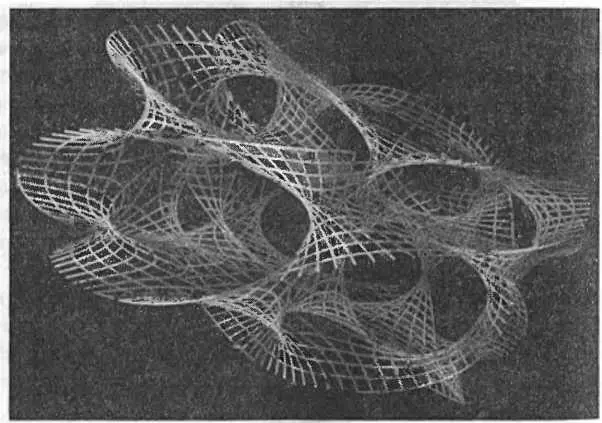
Я попробую дать вам некоторое представление о том, на что похоже обычное пространство, когда к каждой его точке добавлено шестимерное многообразие Калаби — Яу. Сначала посмотрите на обычные измерения, в которых могут двигаться такие большие объекты, как люди. (Я нарисовал его двумерным, но вы уже должны научиться достраивать третье измерение в воображении.)

В каждой точке трехмерного пространства имеется также шесть других свернутых измерений, в которых могут перемещаться очень маленькие объекты. По необходимости я рисую пространства Калаби — Яу отдельно друг от друга, но вы должны представлять себе их в каждой точке обычного пространства.

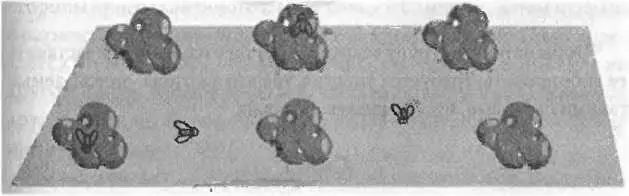
Теперь вернемся к струнам. Обычный жгут от эспандера можно растягивать в разных направлениях, например вдоль оси восток — запад, или север — юг, или верх — низ. Его можно растягивать под разными углами, скажем, на север-северо-запад с 10-градусным наклоном к горизонту. Но если есть дополнительные измерения, число возможностей многократно возрастает. В частности, струны Могут растягиваться вдоль свернутых измерений. Замкнутая струна Может опоясывать пространство Калаби — Яу один или несколько Раз, но при этом вовсе не быть растянутой в обычных пространственных направлениях.

Позвольте мне еще немного усложнить ситуацию. Струна может опоясывать свернутое пространство и в то же самое время извиваться, подобно змее, так что изгибы прокатываются по струне.

Чтобы натянуть струну вокруг свернутого измерения и заставить ее вибрировать, требуется энергия, так что частицы, описываемые такими струнами, будут тяжелее обычных.

Наша Вселенная — это мир не только пространства, времени и частиц, но также и сил. Электрические силы, действующие между заряженными частицами, могут перемещать кусочки бумаги и пылинки (скажем, за счет статического электричества), но более важно, что эти силы удерживают электроны на их орбитах вокруг атомных ядер. Гравитационные силы, действующие между Землей и Солнцем, удерживают на орбите Землю.

Все силы в конечном счете связаны с микроскопическими силами, действующими между отдельными частицами. Но откуда берутся эти межчастичные силы? Для Ньютона универсальная силапритяжения, действующая между массами, была просто физическим фактом — в действительности он смог ее только описать, но не объяснить. Однако в течение девятнадцатого и двадцатого столетий такие физики, как Майкл Фарадей, Джеймс Клерк Максвелл, Альберт Эйнштейн и Ричард Фейнман, сделали блестящие открытия, объяснявшие силы через стоящие за ними более фундаментальные концепции.

Согласно Фарадею и Максвеллу, электрические заряды притягиваются и отталкиваются не непосредственно; в пространстве между зарядами существует посредник, передающий взаимодействие. Представьте себе «Слинки» — эту ленивую игрушечную пружинку, — натянутую между двумя разнесенными на некоторое расстояние шарами.

Каждый из шаров подвергается воздействию силы только со стороны присоединенного к нему конца «Слинки». Затем каждый фрагмент «Слинки» воздействует на своих соседей. Сила передается по «Слинки», пока не передаст натяжение к объекту на другом конце. Может казаться, что два объекта притягиваются друг к другу, но это иллюзия, созданная посредничающей между ними «Слинки».