Марат Телемтаев - Целостный метод – теория и практика

Для оптимального гамильтонова цикла справедливо следующее условие оптимальности: для любого простого маршрута, являющегося участком оптимального гамильтонова цикла и проходящего вершины графа в последовательности i 1, i 2, i 3, …,i a, ( a=4,5, …,n; i l=1,2, …, n ) сумма весов входящих в него ребер μ ( i 1 i 2 i 3…, i a ) является минимальной в сравнении с любой другой суммой вида μ ( i 1i΄ 2i΄ 3…i΄ a-1i a ) :

μ ( i 1 i 2 i 3… i a ) = min μ ( i 1i΄ 2i΄ 3…i΄ a-1i a ) (1)

при a =4, 5, …, n; i=1,2, …, n; i΄ 2, i΄ 3,…, i΄ a-1, ∈P.

Здесь i΄ 2, i΄ 3,…, i΄ a-1— одна из перестановок чисел i 2, i 3, …, i a-1 , P — множество всех перестановок этих чисел.

Очевидно, что если это условие не выполняется для каких-либо значений a и i, то существует гамильтонов цикл с меньшей длиной пути обхода вершин i 1, i 2, i 3, …, i a-1,i a. Но, если полученный гамильтонов цикл оптимален, то его нельзя улучшить изменением пути обхода вершин i 1, i 2, i 3, …, i a для любого a, имеющего значения в пределах от 4-х до n .

Значения a не могут быть меньше четырех, так как очевидно, что никакие два гамильтонова цикла не могут отличаться менее, чем тремя ребрами, проходящими четыре вершины поcледовательно в одном из двух возможных вариантов обхода: i 1,i 2,i 3,i 4 или i 1,i 3,i 2,i 4 .

Пусть оптимальный гамильтонов цикл обходит вершины графа в последовательности

i 1, i 2, i 3, …, i n, i 1. (1.а)

Гамильтонов цикл, оптимальный для определенного значения a, назовем a-оптимальным . Для a = 4 справедливо неравенство:

μ ( i ki k+1 ) + μ ( i k+1i k+2 ) + μ ( i k+2i k+3 ) ≤ μ ( i ki k+2 ) + μ ( i k+2i k+1 ) + μ ( i k+1i k+3 ). (2)

Условие (2) необходимо проверить для всех i k = i 1, i 2, …, i n и, если оно для всех i k справедливо, то это необходимое и достаточное условие того, что гамильтонов цикл 4-оптимален . Просуммировав левые и правые части неравенств, получающихся при значениях i k = i 1, i 2, …, i n, получаем необходимое условие 4-оптимальности в виде:

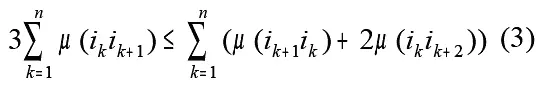
Справедливо следующее условие:

Если гамильтонов цикл a 1-оптимален , то он a 2-оптимален для любого a 21. Если это условие не выполняется, т.е. a 1-оптимальный гамильтонов цикл не является a 2-оптимальным , то какой-то из простых путей длины a 1 можно улучшить изменением обхода каких-то a 2 вершин, что противоречит условия a 1-оптимальности.

Перейдем к определению условия a-оптимальности , получаемого аналогично тому, как условие (З) получено из (2), из системы неравенств вида (2), для любого a=const суммированием для всех i k=1, 2, …, n

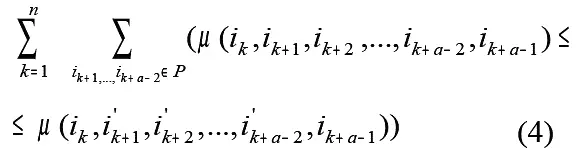
Для каждого значения k будет иметь место система из ((а-2)!-1) неравенств по числу элементов множества Р , состоящего из ( а-2 ) ! перестановок чисел i΄ k+1 , i΄ k+2 , …, i΄ k+a-2

При этом мы полагаем, что

μ ( i k,i k+1 , …, i k+a-1 ) = μ ( i k, i k+1 ) + μ ( i k+1i k+2 ) + … + μ ( i k+a-2i k+a-1 ).

μ ( i k, i΄ k+1 , …, i΄ k+a-2 , i k+a-1 ) = μ ( i k, i΄ k+1 ) + μ ( i΄ k+1 , i΄ k+2 ) + … + μ ( i΄ k+a-2 , i k+a-1 ).

Обозначим левую и правую части условия (4) буквами А и В , соответственно: А ≤ В .

В левой части неравенства вес каждого ребра, принадлежащего проверяемому участку гамильтонова цикла, участвует точно по одному разу в каждом неравенстве системы из (( a-2 ) !-1 ) неравенств, задаваемых перестановками, принадлежащими множеству Р , при фиксированной начальной вершине.

Кроме этого, при заданном a=const , если производить проверку выполнения условия (9.2.4), изменяя последовательно номер начальной вершины от i 1 до i n, то любое ребро гамильтонова цикла появится точно в ( a-1 ) системах из этих (( a-2 ) !-1 ) неравенств как первое по счету, второе, третье и т.д. ( a-1 ) -e ребро в проверяемых участках гамильтонова цикла.

Следовательно, левая часть неравенства (4) имеет вид:

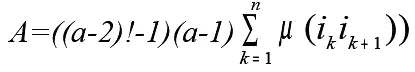
Выражение для правой части условия (4) можно записать в виде:

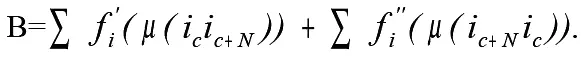
Для того, чтобы получить выражение для правой части условия (4), необходимо найти число появлений ребер графа вида ( i c, i c+N ) в каждой системе из (( a-1 ) !-1 ) неравенств, задаваемых определенным значением k ,а также во всех системах этих неравенств, получаемых при изменении i k от i 1 до i n .

Очевидно, что число появлений пар ( i с, i c+N ) в правых частях неравенств вида (4) равно числу появлений пар ( i c, i c+N ) в последовательностях:

i k, i΄ k+1 , i΄ k+2 , …, i΄ k+a-2 , i k+a-1 (5)

задаваемых ( a-2 ) ! перестановками чисел i΄ k+1 , i΄ k+2 , …, i΄ k+a-2 .

Следует учесть также, что одна из этих последовательностей, а именно i 1, i 2, i 3, …, i k+a-1 находится в левой части этих неравенств.

Пары i ci c+N можно разделить на следующие виды по признаку, содержат они или нет «неподвижные» вершины i k и i k+a-1 :

а) i ci c+N при c ≠ k; c + n < k+a-1; n > 1, n ≤ a-2; это пары элементов в (5), не содержащие элементов i k, i k+a-1 и тех элементов ( i 1, i 2, i΄ 2, i 3, i΄ 3, i 4 и т.д.), которые входят в гамильтонов цикл (1a).

Каждая из пар этого вида появится в системе неравенств (4) для определенного значения i k=i 1,i 2, …, i n , точно ( a-3 )( a-4 ) ! раз – по числу ( a-4 ) ! перестановок ( a-4 ) элементов, т.е. элементов последовательности (5) за вычетом элементов i k, i k+a-1, i c, i c+N для каждого из ( a-3 ) возможных положений пары i c, i c+N в последовательности (5).

б) i c, i c+N при n>1, c=k и i c+Ni c+a-1 при n < а-2, c=k это пары элементов в (5), содержащие элементы i k или i k+a-1 и элементы гамильтонова цикла (1a).

Каждая из этих пар появится в системе неравенств (4) для определенного значения i k=i 1,i 2, …, i n, точно ( a-3 ) ! раз по числу возможных перестановок ( a-3 ) элементов, т.к. элементы i k, i k+N, i k+a-1 для этих пар «неподвижны».

Кроме этого, в совокупностях пар обоих видов надо выделить пары i c, i c+1, т.е. пары элементов гамильтонова цикла (1а). Тогда можно считать, что каждая из этих пар появится в системе неравенств (4) для определенного значения i k=i 1,i 2, …, i n точно (( a-3 ) !-1 ) раз по числу появлений пар вида а) или б) и за вычетом появлений одной пары, находящейся в левой части неравенства (4).