Владимир Кирсанов - Научная революция XVII века

Результат, полученный Галилеем, имел далеко идущие последствия. Поскольку вес и плотность, как было доказано, не оказывают влияния на свободное падение, стало возможным чисто кинематическое рассмотрение падения в терминах пути, времени, скорости и ускорения. Как указывает Макмаллин, «никогда ранее не было ясно, как мертоновская кинематическая геометрия может быть использована для исследования реального падения, поскольку невозможно было взять в расчет такие негеометрические величины, как вес и плотность. А предполагалось, что именно эти параметры определяют естественное движение — падение согласно формуле F/R . Показав, «что ускорение падения не зависит от веса, Галилей доказал применимость геометрического подхода к кинематике» [6, с. 17].

После того, как в дискуссиях Первого дня было показано, что падение тел не зависит ни от их веса, ни от — в идеальном случае — среды, Галилею представляется возможность рассматривать характеристики падения — скорость, ускорение и пройденный путь как чисто геометрические понятия. В Третьем дне он анализирует динамические закономерности, выводя их из чисто кинематических представлений. Так он приходит к доказательству закона падения, а в следующем, Четвертом дне — к закону параболического движения брошенного тела.

Как-то Макс Джеммер остроумно заметил, что «в новейшей теории первоначальные положения и аксиомы, несмотря на то, что они логически предшествуют выводам, эпистемологически следуют за ними» [24, с. 691]. Именно так поступает Галилей в выводе закона падения: он уже давно знает конечный результат и начинает его доказывать с помощью положения, которое эпистемологически, в развитии его творческой мысли, следовало из уже найденной им квадратичной зависимости. Речь идет о правиле средней скорости, которое хорошо уже было знакомо математическим схоластикам XIV в. и получило в дальнейшем известность как «мертонское правило».

Этот факт послужил основанием Пьеру Дюэму утверждать, что Галилей лишь переформулировал то, что было сделано два столетия до него Оремом. То, что такое утверждение неправильно, обусловливается, во-первых, тем, что Галилей пришел к закону падения, исходя не из мертонского правила, а из евдоксовой теории пропорций, а во-вторых, ученые Парижской школы, равно как и калькуляторы Оксфорда, никогда не применяли это правило к случаю действительного падения тел, или даже вообще к случаю любого действительного движения. Мертонское правило оставалось для них абстрактной закономерностью, применяемой в рамках теории интенсификации и ремиссии качеств. Аннелизе Майер подчеркивает, что для ученых Средневековья было чрезвычайно характерно понимание различия между тем, что мы наблюдаем в действительности, и тем, как мы говорим о том, что наблюдаем [1, с. 30]. В связи с этим существовало два подхода к понятию скорости. «С одной стороны, скорость можно было рассматривать как расстояние, проходимое в определенное время. Такое представление хорошо согласовалось не только с эмпирическим восприятием движения, но также и общим определением «velocitas». С другой стороны, скорость могла рассматриваться в контексте теории качеств как интенсивность движения» [1, с. 38].

Галилей был первым, кому пришла в голову мысль объединить эти два подхода. Суть того, что позднее будет названо «мысленным экспериментом», в этом и состоит. Конфигурации качеств Орема и его геометрическая интерпретация мертонского правила обрели у Галилея физический смысл. Обратимся теперь к тексту «Бесед».

Весь анализ падения основывается на следующем утверждении: «Теорема I. Предложение I. Время, в течение которого тело, вышедшее из состояния покоя и движущееся равномерно-ускоренно, проходит некоторое расстояние, равно времени, в течение которого это же расстояние было бы пройдено тем же телом при равномерном движении, скорость которого равняется половине величины наибольшей конечной скорости, достигаемой при первом равномерно-ускоренном движении» [16, II, с. 248].

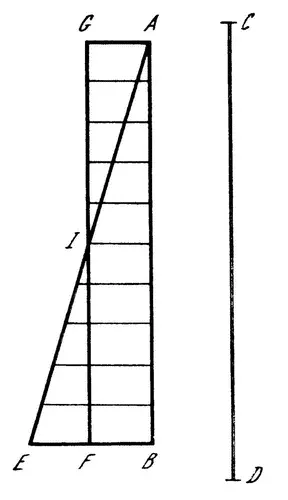
Галилей доказывает это утверждение с помощью чертежа, весьма напоминающего чертеж Орема. Но здесь уже нет никаких неясностей относительно того, что представляют собой элементы Срисованной фигуры. Итак, отрезок прямой АВ представляет время, в течение которого тело проходит путь CD; горизонтальные отрезки, заключенные внутри треугольника ЛЕВ изображают скорость равноускоренного движения, соответствующую любому данному моменту времени (в начале движения скорость равна нулю, в конце — своей максимальной величине ЕВ). При этом ясно, что путь, пройденный телом, будет изображаться площадью треугольника AEB (Галилей говорит здесь о «сумме», или «совокупности» линий, заключенных внутри треугольника). Аналогичным образом прямоугольник AGFB представляет собой путь, пройденный тем же телом в равномерном движении со средней скоростью FB = ½∙EB. Желаемое равенство времен следует из равенства треугольников IGA и IEF. Равенство треугольников означает равенство путей: «Отсюда следует, что два тела пройдут равные расстояния в одно и то же время, если одно, выйдя из состояния покоя, будет двигаться равномерно-ускоренно, а другое просто равномерно со скоростью, равною половине максимальной скорости, достигнутой при ускоренном движении, что и требовалось доказать» [16, II, с. 249].

Затем Галилей обращается непосредственно к доказательству квадратичной зависимости пути от времени. В нем он опирается на другое положение, выдвинутое им ранее, а именно, что скорость падения пропорциональна времени падения. Трактовка доказательства этого положения, данного в «Беседах», заслуживает отдельного рассмотрения, поскольку она является ошибочной в большинстве историко-научных работ, посвященных этому вопросу.

К моменту написания «Бесед» Галилей уже давно пришел к ясному пониманию скорости движения, а следовательно, и к пониманию того, что скорость падения пропорциональна времени. Все это, как показано выше, еще не было достигнуто тогда, когда он впервые пришел к установлению квадратичной зависимости пути от времени около 30 лет назад. И вот, в «Беседах» он специально останавливается на выборе альтернативы: чему пропорциональна скорость — времени или пути, и отвергает второе предположение с помощью следующего доказательства от противного:

«Если бы скорости были пропорциональны пройденным или имеющим быть пройденными расстояниям, то такие расстояния проходились бы в равные промежутки времени; таким образом, если бы скорость, с которой падающее тело проходит расстояние в четыре локтя, была вдвое больше скорости, с которою оно проходит расстояние в первых два локтя (на том основании, что одно расстояние вдвое больше другого), то промежутки времени для прохождения того и другого расстояния должны были бы быть одинаковыми. Но прохождение одним и тем же телом четырех локтей и двух локтей в один и тот же промежуток времени могло бы иметь место лишь в том случае, если бы движение проходило мгновенно; мы же видим, что падающее тело совершает свое движение во времени и что два локтя оно проходит в меньший срок, нежели четыре локтя. Следовательно, утверждение, что скорости растут пропорционально пройденным путям, ложно» [16, II, с. 245].