И. Константинов - Сборка кубика Рубика
- Название:Сборка кубика Рубика
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:1983
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
И. Константинов - Сборка кубика Рубика краткое содержание
Часть статьи из журнала № 5 "Наука и жизнь" за 1983 год
Сборка кубика Рубика - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Пятый этап
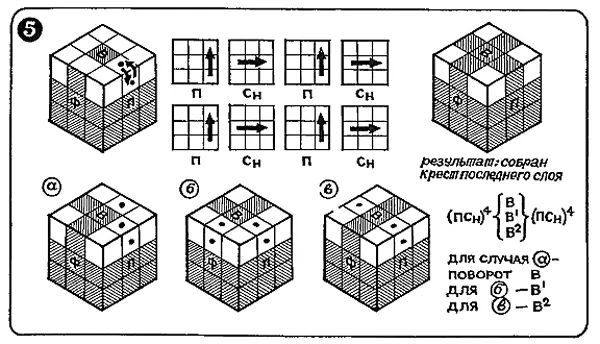
Ориентирование двух бортовых кубиков по Д. Конвею. Очень простой, легко запоминающийся процесс, но именно здесь у некоторых читателей возникли трудности. Здесь следует учесть: разворачиваемый кубик должен быть на правой грани, на рисунке он помечен стрелками. На рисунках а), б), и в представлены возможные случаи расположения неверно ориентированных кубиков (помечены точками). Используя общую формулу в случае а), потребуется выполнить промежуточный поворот В, чтобы вывести второй кубик на правую грань, а в случаях б) и в) соответственно В' и В².
Многих смущало то, что после первой части процесса (ПС н) 4нужный кубик разворачивался как надо, но порядок в собранных слоях нарушался. Это сбивало с толку и заставляло бросать на полпути почти собранный куб. Выполнив промежуточный поворот, не обращая внимания на поломку нижних слоев, проделайте операции (ПС н) 4второй части процесса, и все станет на свои места. Результат: собран крест.
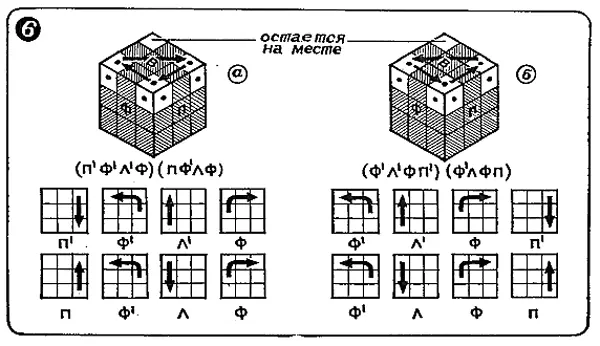
Шестой этап
Углы последней грани возможно поставить на свои места, используя не 22-ходовый процесс, описанный в № 2, 1982 года, а 8-ходовый, удобный для запоминания, — прямой, переставляющий три угловых кубика в направлении по часовой стрелке, и обратный, переставляющий три кубика в направлении против часовой стрелки.
После пятого этапа, как правило, хотя бы одни кубик да сядет на свое место, пусть и неправильно ориентированно. Поверните куб так, чтобы этот кубик оказался в левом дальнем углу, и повторите процесс еще раз-два, пока все кубики не станут на свои места. Результат: все угловые кубики заняли свои места, но два из них (а может, и четыре) ориентированы неправильно.
Седьмой этап
Ориентация угловых кубиков последней грани. Процесс тоже очень легко запомнить — это многократно повторяемая последовательность поворотов ПФ'П'Ф.
Поверните куб так, чтобы кубик, который вы хотите развернуть, был в правом верхнем углу фасада. 8-ходовый процесс (2x4 хода) повернет его на ¹/з оборота но часовой стрелке. Если при этом кубик еще не сориентировался, повторите 8-ходовку еще раз (в формуле это отражено индексом «п»).
Не обращайте внимания на то, что нижние слои при этом придут в беспорядок: ситуации аналогична проделанной на пятом этапе, она тоже парная, разбивается на дпе идентичные половники с промежуточной операцией поворота верхней грани Выполнение лраной части процесса автоматически приводит в порядок нарушенную гармонию
На рисунке показаны трн случая расположения «плохих» кубиков (они помечены точками). В случае а) требуется промежуточный поворот В, а в случае б) — поворот В' и в случае в) — поворот В 2. Результат: последняя грань собрана.
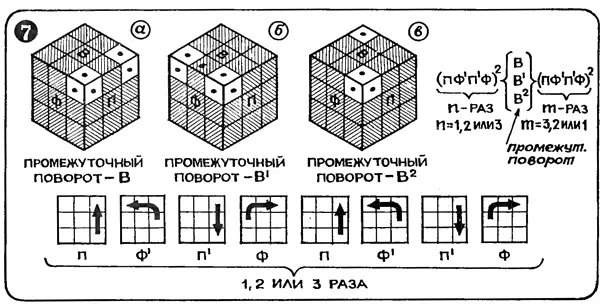
Теперь остается лишь повернуть ее, и все — куб собран, хлопайте в ладошки!
ПАСЬЯНСЫ НА КУБИКЕ
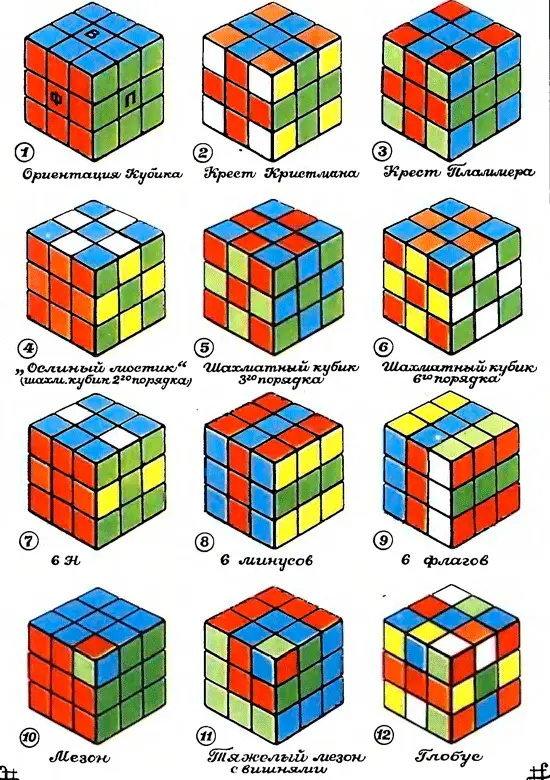
Первоначальная ориентация куба: верх — синий, фасад — красный, справа — зеленый, слева — желтый, низ — белый, тыл — оранжевый
Ослиный мостик (шахматный кубик 2-го порядка) (№ 4) — С² пС² нС² ф.
Точки — С' нС' пС нС п.
Крест Кристмана (№ 2) — П'(С² пС² фВ²С² пС² ФН²)П.
Крест Пламмера (№ 3) — О² ф[О ф(В²С² ПВ С² пВ²С² фН'С² ф)]².
Шахматный кубик 3-го порядка (№ 5) — [(С² фНС² фВ²С² пВ'С² пВ²)О' ф]²О² ф•(С' пС' нС пС н) • О пО в•С² пС² фС² н.
Эта фигура представляет собой сочетание фигур «Крест Пламмера» и «Точки».
Шахматный кубик 6-го порядка — сочетание алгоритмов шахматного кубика 3-го порядка и «Ослиного мостика» (№ 6) —
[(С² фНС² фВ²С² ПВ'С² пВ²)О' ф]² О² ФС' пС' НС пС п•О пО в•С² пС² фС² н
Фигура «6Н» (№ 7) — Н²С пС² фС' пВ² О² в.
Фигура «6 минусов» (№ 8) — П²Ф²С²пТ²Л²О п²С пО' п
6 флагов (№ 9) — В'Т²Л²ВС² пВ'П²Ф²НФТПС пП'Т'П'С нП²С' нП'Ф' Т²П²Т²Ф²С фО фО в(Г. Галл).
Мезон («кварк — антикварк») (№ 10)
Л²П'НП ФНФ' В' • ФН'Ф' • П'Н'П • В • Л².
Гигантский мезон — Ф'В'ТВ²ВПВ²П'Ф ТНФ'Н²ФН'Л'Н²ЛТ' (Д. Сингмайстер).
Гигантский мезон с вишнями (№ 11) — П'В²НТ'С нТ²С' нТ'В²Н'П ЛН²В'ФС нФ²С' нФН²ВЛ'С' нС' пС пС п.
Глобус (№ 12) — (ФТЛП)²ЛП. Фигура, придуманная Д. Максвеллом, представляет собой «глобус»», на котором расположены 54 страны, и ни одна из иих не соприкасается протяженными границами со страной, совпадающей по цвету иа глобусе.
Редакция благодарит И. Белова (г. Москва), В. Гаврилец (г. Калинин), М. Ганшина (г. Москва), В. Гурина (г. Севастополь), А. Ев-сюкова (г. Калининград), И. Индриксона (г. Рига), Е. Клиссанича (г. Ленинград), Ю. и Д. Кошелевых (г. Москва), А Кура (г. Ленинград), Р. Терехова (г. Уфа), А. Чува-сова (г. Тула) и других читателей, приславших интересные сообщения о придуманных ими алгоритмах сборки кубика и решивших предложенные аадачи-пасьянсы
Интервал:
Закладка:








